Ratio-Based Modified Logistic Isothermal Microbial Growth

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
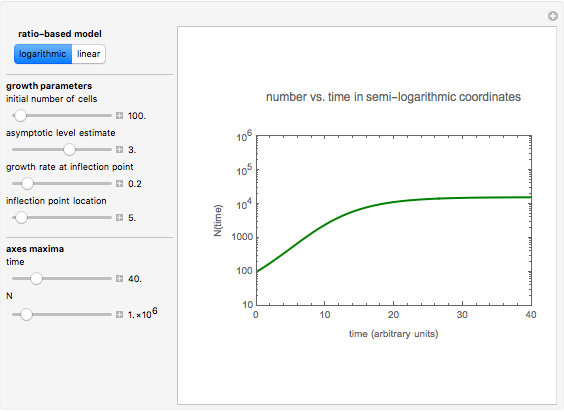
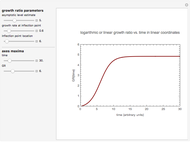
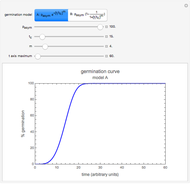
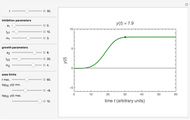
This Demonstration contains two kinds of plots generated by two different ratio-based logistic models. They produce growth curves plotted on semi-logarithmic and linear coordinates. Each simulates the rise of a microbial population's number, N(time), in a food at constant temperature. Choose which model to use with the displayed selector switch. You can modify the plotted growth curve by slider-controlled setting of the underlying model equation's four parameters.
Contributed by: Mark D. Normand and Micha Peleg (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
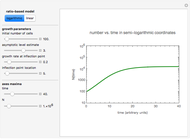
Snapshot 1: growth curve with no logarithmic lag time produced by a logarithmic ratio-based model (plotted on semi-logarithmic coordinates)
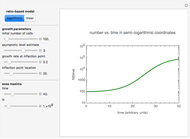
Snapshot 2: growth curve with a short logarithmic lag time produced by a logarithmic ratio-based model (plotted on semi-logarithmic coordinates)
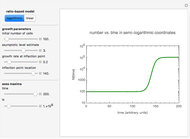
Snapshot 3: growth curve with an extremely long logarithmic lag time produced by a logarithmic ratio-based model (plotted on semi-logarithmic coordinates)
Snapshot 4: growth curve with no lag time produced by a linear ratio-based model (plotted on linear coordinates)
Snapshot 5: growth curve with a short lag time produced by a linear ratio-based model (plotted on linear coordinates)
Snapshot 6: growth curve with an extremely long lag time produced by a linear ratio-based model (plotted on linear coordinates)
This Demonstration contains two kinds of growth curves:
a) a semi-logarithmic plot of the rise in the number of cells produced by a logarithmic ratio-based version of the logistic function formulated as  . The growth ratio itself is defined as
. The growth ratio itself is defined as 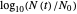 , where
, where 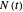 is the actual number (count) and
is the actual number (count) and 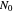 is the initial number of cells.
is the initial number of cells.
b) a linear plot of the rise in the number of cells produced by a linear ratio-based version of the logistic function formulated as  . The growth ratio itself,
. The growth ratio itself, 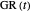 , is defined as
, is defined as 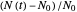 , where
, where 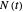 is the actual number (count) and
is the actual number (count) and 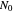
 is the initial number of cells.
is the initial number of cells.
In both models, at  , the ratio is also zero. The Demonstration can be used to model isothermal microbial growth in foods by slider-controlled manipulation of four growth parameters: the initial number of cells,
, the ratio is also zero. The Demonstration can be used to model isothermal microbial growth in foods by slider-controlled manipulation of four growth parameters: the initial number of cells, 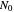 , an estimate of the asymptotic growth ratio,
, an estimate of the asymptotic growth ratio, 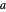 , the normalized rate at the curve's inflection point,
, the normalized rate at the curve's inflection point,  , and the inflection point's location,
, and the inflection point's location,  . Two other sliders control the maximum settings of the time and number of cells axes.
. Two other sliders control the maximum settings of the time and number of cells axes.
The logarithmic ratio-based model is particularly suitable for generating growth curves with a long logarithmic lag time for which the conventional Verhulst model is inappropriate and where the increase in the number of cells covers several orders of magnitude. The linear ratio-based model is particularly suitable for generating growth curves with a long lag time for which the conventional Verhulst model is inappropriate and where there is only a several-fold increase in the number of cells. The generated plots are similar to those produced by the Gompertz model. The main advantage of both models is that each of the parameters has an intuitive meaning and can be varied independently.
Although the scales are set so that most of the generated curves will correspond to observable microbial growth patterns, the program can also be used to model growth phenomena in other areas such as economics.
Please note that not all possible parameter combinations necessarily yield a realistic growth curve.
For more on the model and its application in foods see: M. G. Corradini and M. Peleg, "Estimating Non-Isothermal Bacterial Growth in Foods from Isothermal Experimental Data," Journal of Applied Microbiology, 99(1), 2005 pp. 187-200. M. Peleg, Advanced Quantitative Microbiology for Foods and Biosystems: Models for Predicting Growth and Inactivation, Boca Raton, FL: CRC Press, 2006.
Permanent Citation