Effect of Tube Diameter on Plug Flow Reactor

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
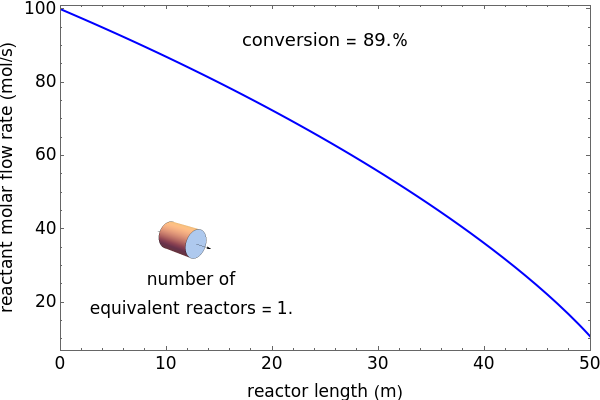
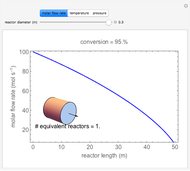
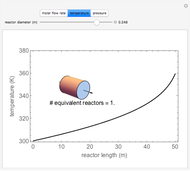
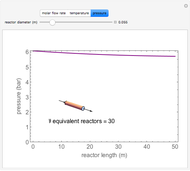
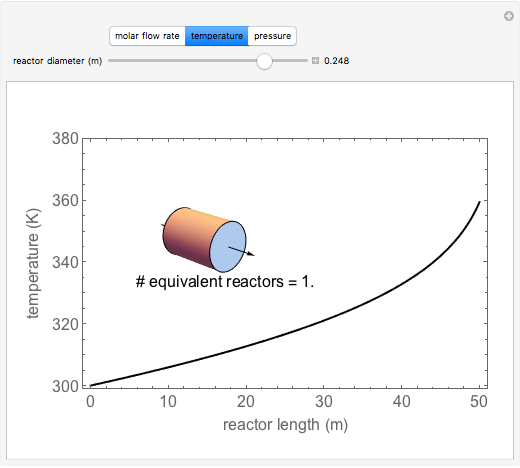
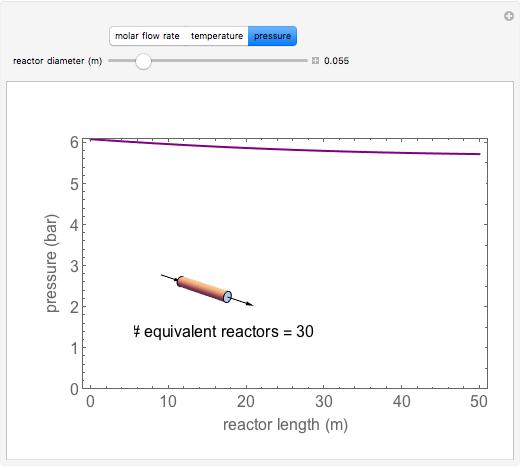
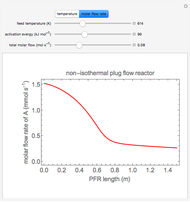
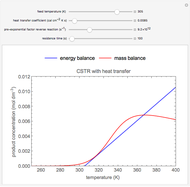
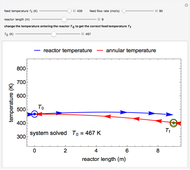
A first-order, exothermic reaction takes place in a plug flow reactor (PFR) that has pressure drop and heat transfer through the walls. Use the slider to observe the effects of changing reactor diameter; the total feed flow rate is kept constant by changing the number of parallel reactors (number of equivalent reactors) so that the total reactor cross section does not change. Use buttons to observe how reactant molar flow rate, temperature, and pressure depend on reactor length. For small-diameter reactors, the pressure drop is higher, which increases the volumetric flow rate and reduces the residence time; this lowers conversion. Since heat transfer is more efficient for smaller-diameter reactors because the surface area per volume is larger, the temperature increases less; this also lowers conversion.
Contributed by: Rachael L. Baumann (April 2014)
Additional contributions by: John L. Falconer and Nick Bongiardina
(University of Colorado Boulder, Department of Chemical and Biological Engineering)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Ergun equation for pressure drop in a plug flow reactor:
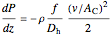 ,
,
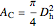 ,
,
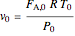 ,
,
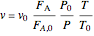 ,
,
where  is pressure (
is pressure (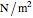 ),
),  is distance down the reactor (m),
is distance down the reactor (m),  is fluid density (
is fluid density ( ),
), 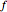 is friction factor,
is friction factor, 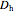 is the hydraulic diameter, which is equal to reactor diameter in absence of heating or cooling (m),
is the hydraulic diameter, which is equal to reactor diameter in absence of heating or cooling (m),  is volumetric flow rate (
is volumetric flow rate (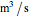 ),
),  is the cross-sectional area of the reactor (
is the cross-sectional area of the reactor ( ),
), 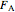 is the molar flow rate of
is the molar flow rate of 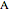 (mol/s),
(mol/s), 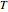 is temperature (K),
is temperature (K), 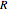 is the ideal gas constant (J/[mol K]), and the subscript
is the ideal gas constant (J/[mol K]), and the subscript  refers to the inlet.
refers to the inlet.
The pipe is assumed to be commercial steel. For laminar flow, the following equation is used to calculate the Darcy friction factor. For turbulent and transitional flow, Serghide's explicit solution to the Colebrook equation is used:
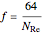 for
for 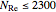 ,
,
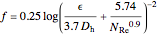 for
for 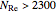 ,
,
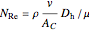 ,
,
 ,
,
where 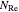 is the Reynolds number,
is the Reynolds number,  is wall roughness (m),
is wall roughness (m),  is dynamic viscosity (kg/[m s]), and
is dynamic viscosity (kg/[m s]), and  is reactor diameter (m).
is reactor diameter (m).
Mass balance:
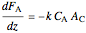 ,
,
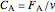 ,
,
where 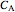 is the reactant concentration (
is the reactant concentration (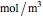 ), and
), and  is the rate law constant (1/s).
is the rate law constant (1/s).
Energy balance:
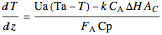 ,
,
where 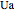 is the heat transfer coefficient times area/volume (
is the heat transfer coefficient times area/volume (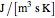 ),
), 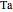 is the temperature of the coolant (K),
is the temperature of the coolant (K),  is heat of reaction (J/mol), and
is heat of reaction (J/mol), and 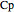 is heat capacity of reactants (J/[mol K]).
is heat capacity of reactants (J/[mol K]).
The screencast video at [1] shows how to use this Demonstration.
Reference
[1] Effect of Tube Diameter on Plug Flow Reactor. www.colorado.edu/learncheme/kinetics/TubeDiameterPFR.html.
Permanent Citation