Roots of Holomorphic Functions in the Unit Disk

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
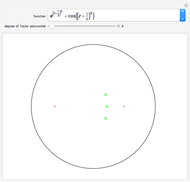
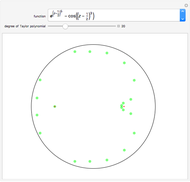
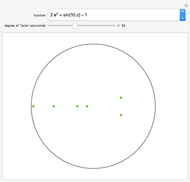
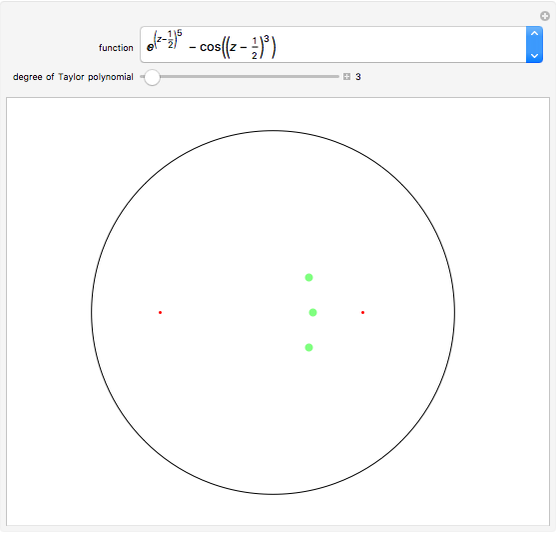
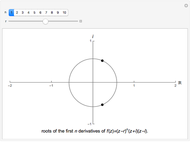
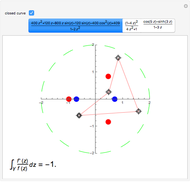
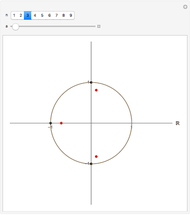
This Demonstration investigates how the roots of the polynomials in the Taylor expansion of a function analytic in the unit disk converge to the roots of the function in the disk. The roots of the selected analytic function are represented by small red points. The roots of the Taylor polynomial of a chosen degree are represented by larger green points. As you increase the degree of the Taylor polynomial, the number of green points may increase or decrease but eventually there will be as many red points as green points in the disk and they will almost coincide.
Contributed by: Andrzej Kozlowski (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
[1] E. C. Titchmarch, The Theory of Functions, London: Oxford University Press, 1952.
Permanent Citation
"Roots of Holomorphic Functions in the Unit Disk"
http://demonstrations.wolfram.com/RootsOfHolomorphicFunctionsInTheUnitDisk/
Wolfram Demonstrations Project
Published: March 7 2011