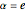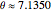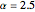The Frank-Kamenetskii Problem Using Arc-Length Continuation
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
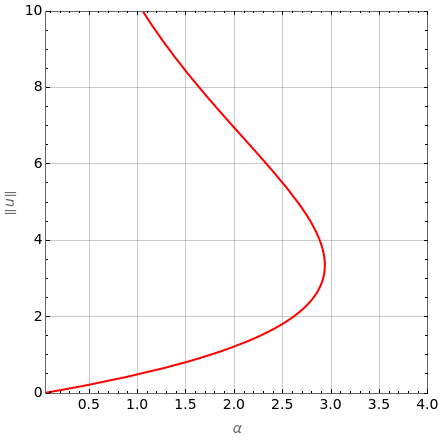
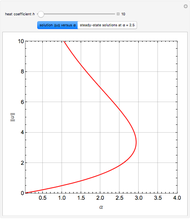
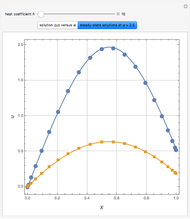
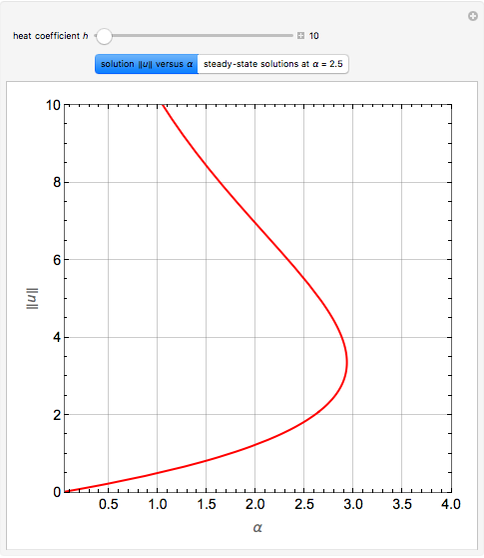
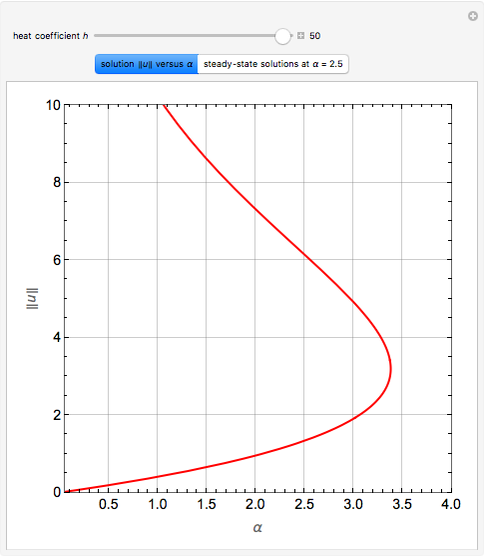
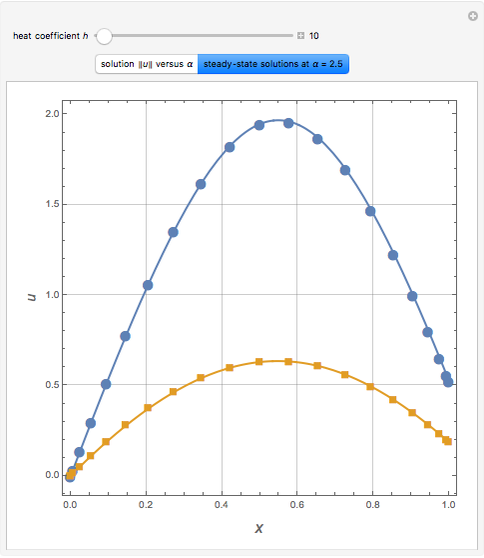
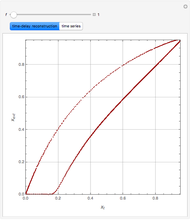
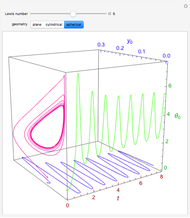
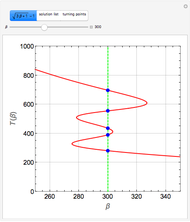
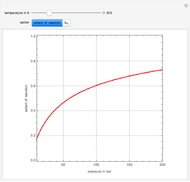
The Frank–Kamenetskii problem relates to the self-heating of a reactive solid. When the heat generated by a reaction is balanced by conduction in a one-dimensional slab of combustible material, the nonlinear boundary value problem (BVP)  for
for  ,
,  , and
, and  admits up to two solutions. Here,
admits up to two solutions. Here,  is the dimensionless temperature and
is the dimensionless temperature and  is the heat transfer coefficient.
is the heat transfer coefficient.
Contributed by: Housam Binousand Brian G. Higgins (December 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation