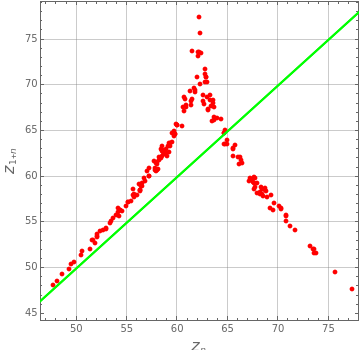
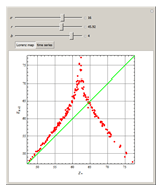
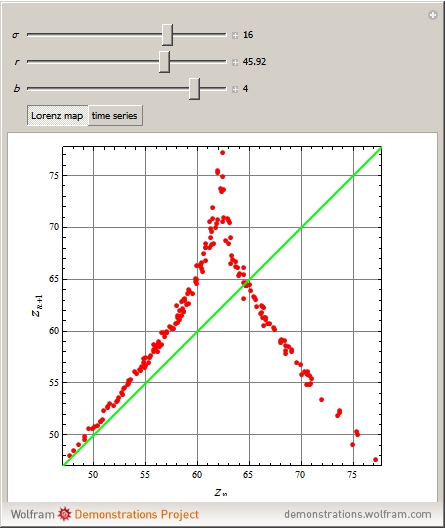
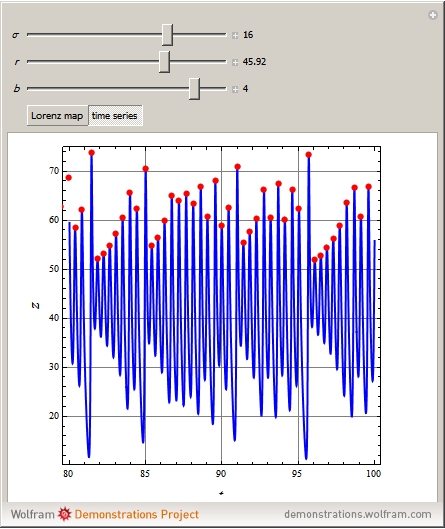
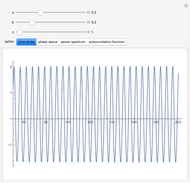
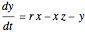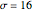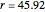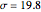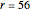The Lorenz Map: Short-Term Predictability of Chaotic Systems
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
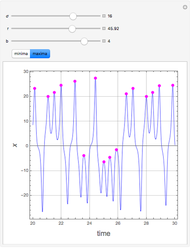
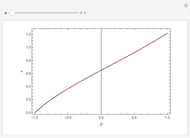
This Demonstration plots a map of the Lorenz system defined by
[more]
Contributed by: Housam Binous, Ahmed Bellagi, and Brian G. Higgins (September 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference
[1] E. N. Lorenz, "Deterministic Nonperiodic Flow," Journal of Atmospheric Science, 20(2), 1963 pp. 130–141. doi: 10.1175/1520-0469(1963)020%3 C0130:DNF %3 E2 .0.CO;2.
Permanent Citation