Arrhenius versus Eyring-Polanyi Model

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
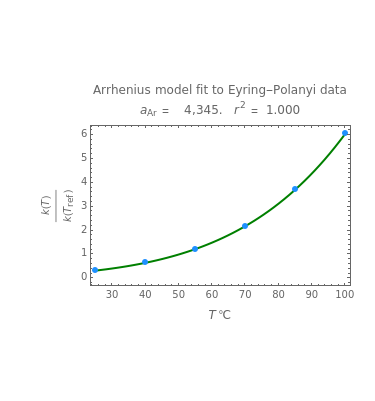
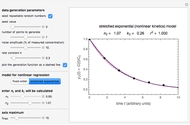
The Arrhenius and Eyring–Polanyi equations are alternative models of the effect of temperature on the rate of chemical reactions and biological processes. This Demonstration generates data with the Arrhenius equation and fits it with the Eyring–Polanyi model and vice versa. It shows that although the two models are derived from different statistical mechanical considerations, they can be used interchangeably over a large range of temperatures. The two models diverge significantly only at very high temperatures: according to the Arrhenius model, the rate approaches an asymptotic value, while according to the Eyring–Polanyi model, it continues to rise. This suggests that curve fitting cannot establish either model's superiority beyond a limited range.
Contributed by: Mark D. Normand and Micha Peleg (March 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Snapshot 1: generated with the Eyring–Polanyi and fitted with the Arrhenius model—low temperatures
Snapshot 2: generated with the Eyring–Polanyi and fitted with the Arrhenius model—very high temperatures
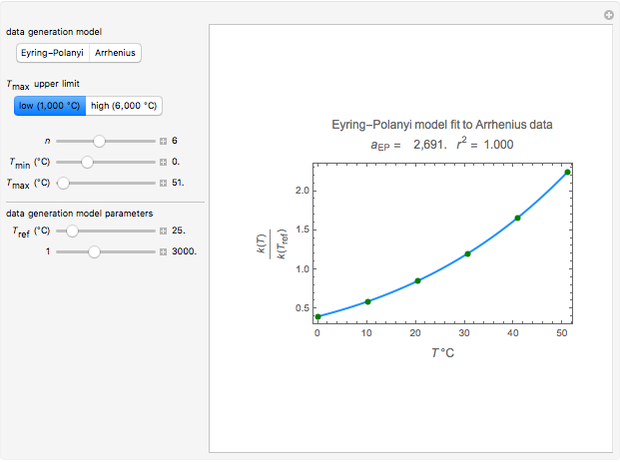
Snapshot 3: generated with the Arrhenius and fitted with the Eyring–Polanyi model—low temperatures
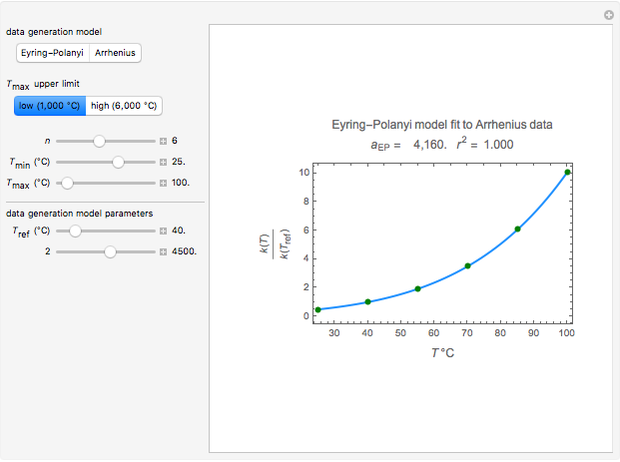
Snapshot 4: generated with the Arrhenius and fitted with the Eyring–Polanyi model—high temperatures
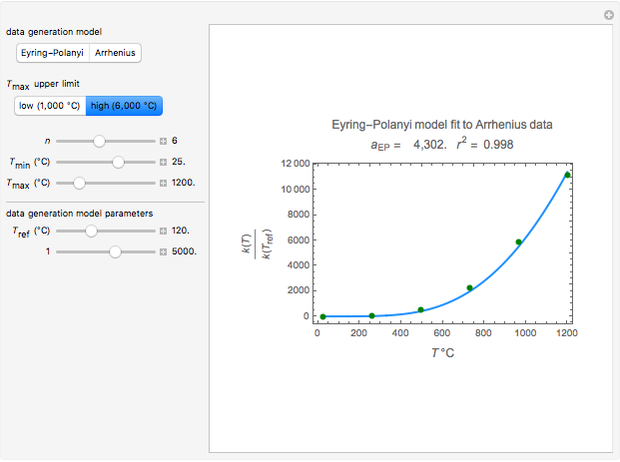
Snapshot 5: generated with the Arrhenius and fitted with the Eyring–Polanyi model—very high temperatures
The effect of temperature on the rate of chemical and biochemical reactions has been primarily described by the Arrhenius equation. It can be written in the form  , where
, where 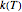 and
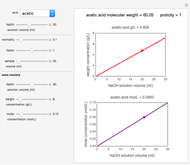
and 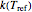 are the rate constants at absolute temperature
are the rate constants at absolute temperature 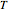 and
and 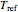 , respectively,
, respectively, 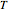 in
in 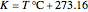 , and
, and 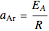 ,
, 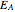 being the activation energy and
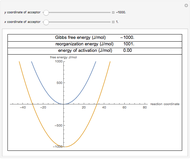
being the activation energy and 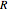 the universal gas constant in the corresponding units. Although derived from statistical mechanics, the Arrhenius model is increasingly being treated as a successful empirical model; see also [1]. An alternative model, also derived from statistical mechanics, is the Eyring–Polanyi equation. It can be written in the form
the universal gas constant in the corresponding units. Although derived from statistical mechanics, the Arrhenius model is increasingly being treated as a successful empirical model; see also [1]. An alternative model, also derived from statistical mechanics, is the Eyring–Polanyi equation. It can be written in the form 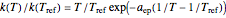 , where
, where 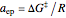 ,
, 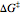 being the Gibbs energy of activation.
being the Gibbs energy of activation.
From a purely formal viewpoint, the main difference between the two models is the term 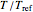 on the right side of the Eyring–Polanyi equation. Consequently, and in contrast with the Arrhenius model, the Eyring–Polanyi model implies that
on the right side of the Eyring–Polanyi equation. Consequently, and in contrast with the Arrhenius model, the Eyring–Polanyi model implies that 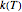 can increase indefinitely, that is, as
can increase indefinitely, that is, as 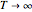 ,
, 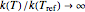 . According to the Arrhenius model, as
. According to the Arrhenius model, as 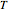 rises, the
rises, the 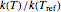 versus
versus 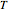 relationship has an inflection point at
relationship has an inflection point at 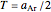 , and as
, and as 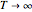 , it approaches an asymptotic value of
, it approaches an asymptotic value of 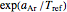 . Also, and again in contrast with the Arrhenius model, the plot of log
. Also, and again in contrast with the Arrhenius model, the plot of log 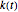 versus
versus 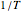 need not be linear.
need not be linear.
This Demonstration generates 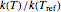 data with the Arrhenius equation and compares them with the Eyring–Polanyi model. The choice is made with a setter bar. You can also select the temperature range, the reference temperature, and the
data with the Arrhenius equation and compares them with the Eyring–Polanyi model. The choice is made with a setter bar. You can also select the temperature range, the reference temperature, and the 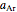 or
or 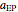 values with a slider.
values with a slider.
The Demonstration plots the generated data points with their fitted curve superimposed. It also displays the fitted parameter value for 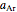 or
or 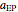 and the regression coefficient,
and the regression coefficient, 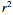 .
.
These plots show that over a wide range of temperatures, the Arrhenius and Eyring–Polanyi equations can be used interchangeably and that they diverge only at very high temperatures, around the Arrhenius equation's inflection point. This suggests that neither model can be considered superior on the basis of curve fitting alone.
It is not the purpose of this Demonstration to match any particular real system, and therefore some combinations of parameter values do not have a real-life 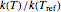 versus
versus 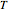 relationship.
relationship.
Reference
[1] M. Peleg, M. D. Normand, and M. G. Corradini, "The Arrhenius Equation Revisited," Critical Reviews in Foods Science and Nutrition, 52(9), 2012 pp. 830–851. doi:10.1080/10408398.2012.667460.
Permanent Citation