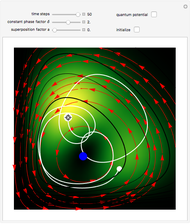
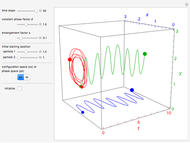
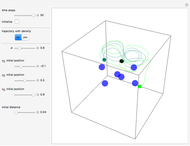
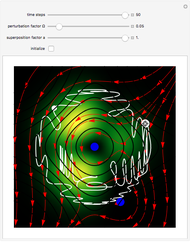
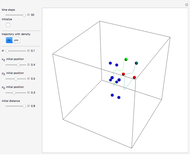
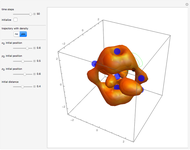
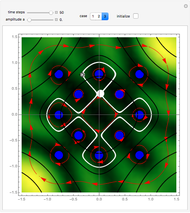
3D Quantum Trajectory for a Particle in a Harmonic Potential

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
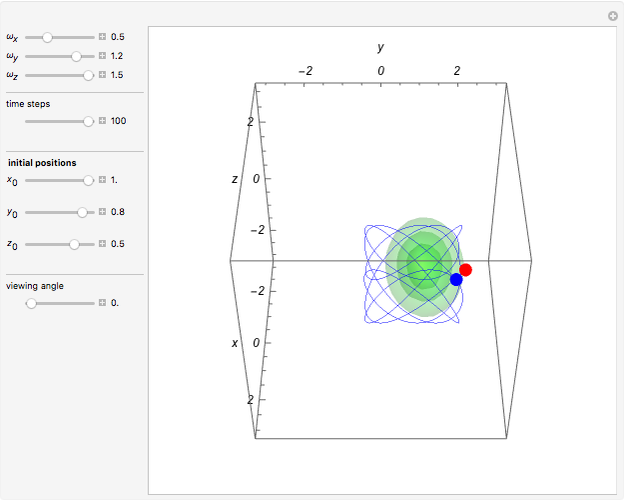
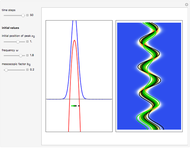
The quantum harmonic oscillator is an example of a nondispersive Gaussian wave packet that oscillates harmonically and is centered around 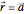 at
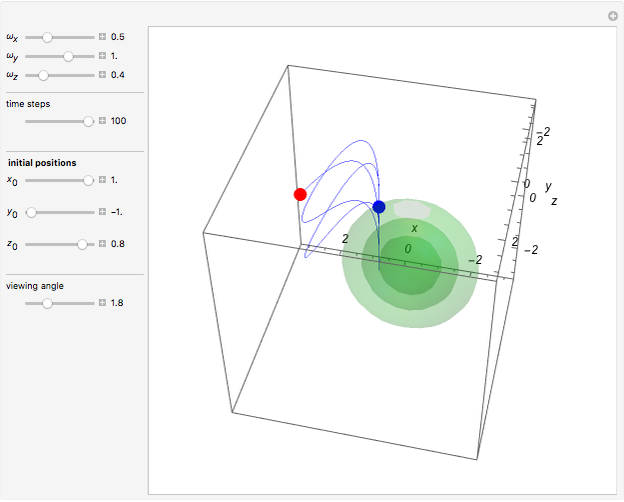
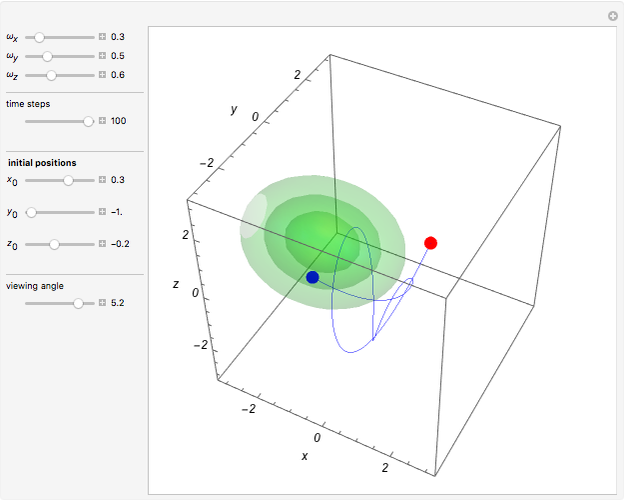
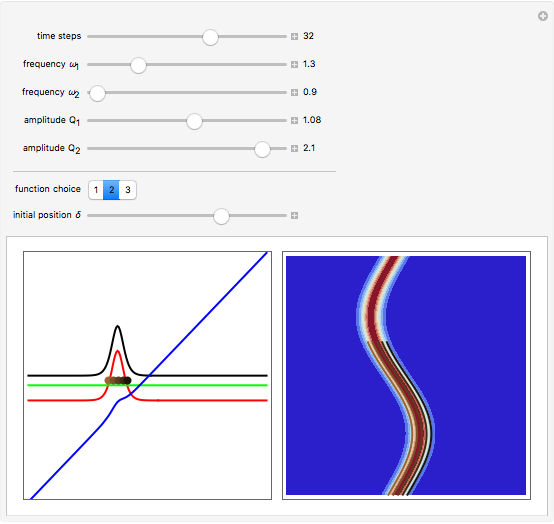
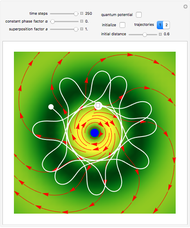
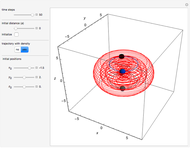
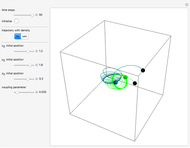
at  . This Demonstration shows the motion of a 3D quantum particle, which could be described by three harmonic oscillators in three-dimensional configuration space (CS). In this case, the independence of the orthogonal motions of the oscillator is assured. Independence of the component motions is maintained if the wavefunction is factorizable in CS.
. This Demonstration shows the motion of a 3D quantum particle, which could be described by three harmonic oscillators in three-dimensional configuration space (CS). In this case, the independence of the orthogonal motions of the oscillator is assured. Independence of the component motions is maintained if the wavefunction is factorizable in CS.
Contributed by: Klaus von Bloh (December 2013)
Open content licensed under CC BY-NC-SA
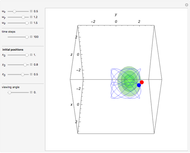
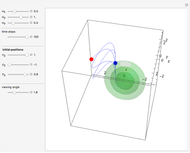
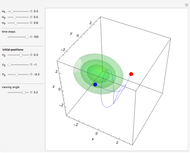
Snapshots
Details
The complete wavefunction (with 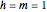 ) is:
) is:
 with
with  , which is in the eikonal form
, which is in the eikonal form  :
:
 ,
,
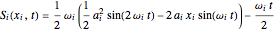 .
.
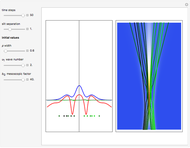
The gradient of the phase 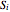 gives the particle velocity field. In this special case, the complete phase function
gives the particle velocity field. In this special case, the complete phase function 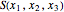 decomposes into a sum
decomposes into a sum 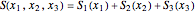 , in which the motions in the three coordinate directions are completely independent. The motion is given by
, in which the motions in the three coordinate directions are completely independent. The motion is given by  , where
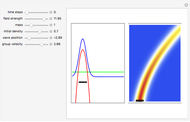
, where  is the initial starting point. The trajectory of the particle oscillates with the amplitude
is the initial starting point. The trajectory of the particle oscillates with the amplitude 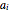 and frequency
and frequency  and forms Lissajous-like curves. The appearance of the figure is highly sensitive to the ratio of the frequencies
and forms Lissajous-like curves. The appearance of the figure is highly sensitive to the ratio of the frequencies  .
.
References
[1] P. Holland, The Quantum Theory of Motion, Cambridge: Cambridge University Press, 1993.
[2] D. Bohm, Quantum Theory, New York: Prentice-Hall, 1951.
Permanent Citation