Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

3D Quantum Trajectory for a Particle in a Harmonic Potential

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

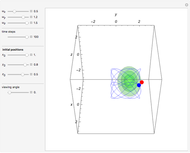
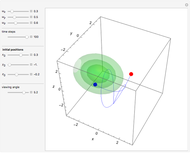
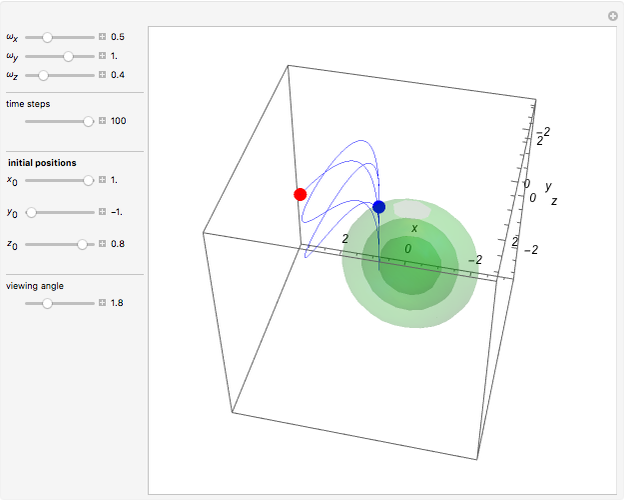
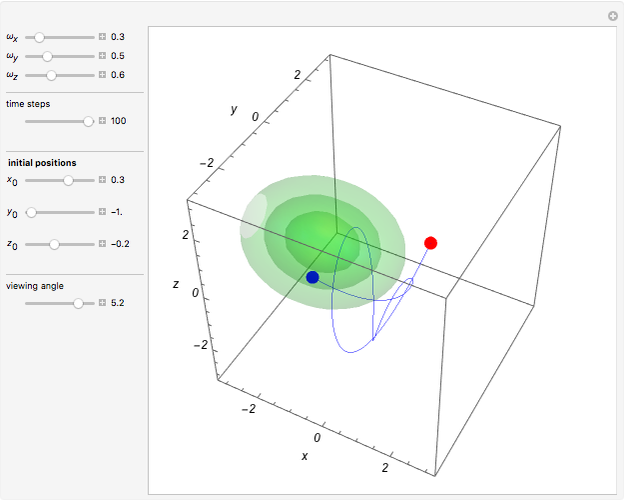
The quantum harmonic oscillator is an example of a nondispersive Gaussian wave packet that oscillates harmonically and is centered around at . This Demonstration shows the motion of a 3D quantum particle, which could be described by three harmonic oscillators in three-dimensional configuration space (CS). In this case, the independence of the orthogonal motions of the oscillator is assured. Independence of the component motions is maintained if the wavefunction is factorizable in CS.

[more]

If factorizability of the wavefunction is not possible, for example because of quantum superposition represented by a product state, the motion becomes entangled, meaning that the motion in one coordinate direction depends on other coordinate directions. If the CS is defined as real space, entanglement is equivalent to quantum nonlocality. Thus in the Bohmian approach, nonlocality is associated with nonfactorizability of the wavefunction.

The graphic shows the squared wavefunction and the trajectory.

[less]

Contributed by: Klaus von Bloh (December 2013)
Open content licensed under CC BY-NC-SA

Snapshots

Details

The complete wavefunction (with ) is:

with , which is in the eikonal form :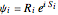

,

.

The gradient of the phase gives the particle velocity field. In this special case, the complete phase function decomposes into a sum , in which the motions in the three coordinate directions are completely independent. The motion is given by 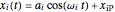, where 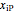is the initial starting point. The trajectory of the particle oscillates with the amplitude and frequency and forms Lissajous-like curves. The appearance of the figure is highly sensitive to the ratio of the frequencies .

References

[1] P. Holland, The Quantum Theory of Motion, Cambridge: Cambridge University Press, 1993.

[2] D. Bohm, Quantum Theory, New York: Prentice-Hall, 1951.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send