Closure Property of Eigenfunctions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
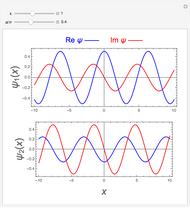
A complete set of discrete eigenfunctions obeys the orthonormalization conditions  . Complementary to these is the set of closure relations
. Complementary to these is the set of closure relations  . For real eigenfunctions, the complex conjugate can be dropped. The finite sums
. For real eigenfunctions, the complex conjugate can be dropped. The finite sums  for
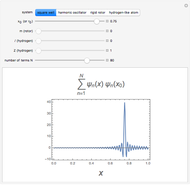
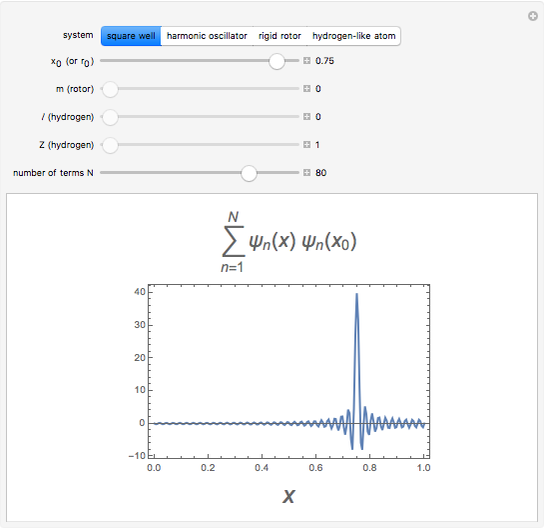
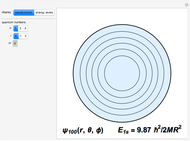
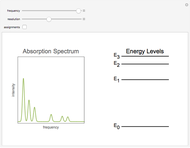
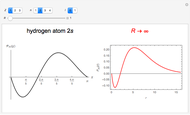
for  up to 100 are evaluated in this Demonstration. Four systems are considered: (1) infinite square-well potential with
up to 100 are evaluated in this Demonstration. Four systems are considered: (1) infinite square-well potential with  and eigenfunctions
and eigenfunctions  ,
,  ,
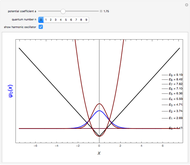
,  ; (2) linear harmonic oscillator with
; (2) linear harmonic oscillator with  and
and  ,
,  ,
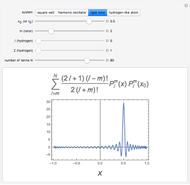
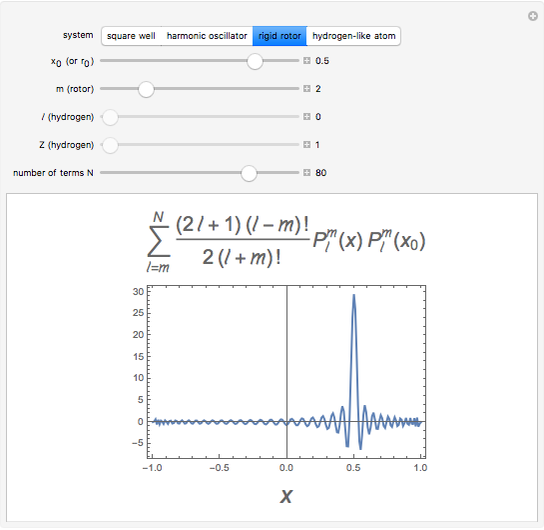
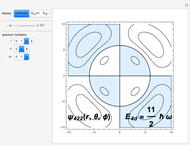
,  ; (3) linear rigid rotor for fixed
; (3) linear rigid rotor for fixed  ,
,  ,
,  ,
,  ,
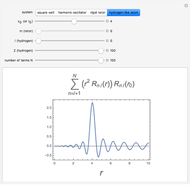
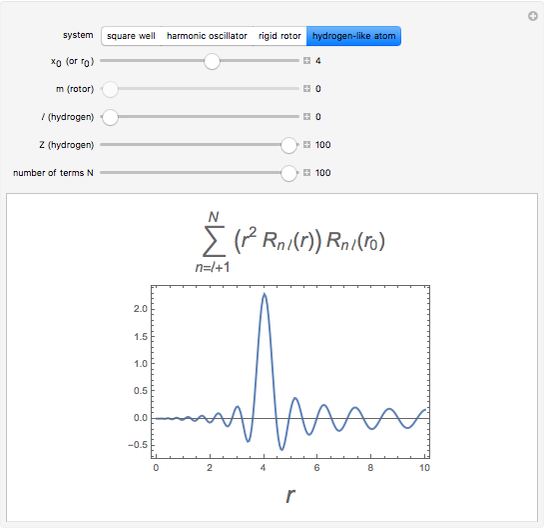
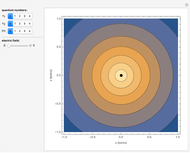
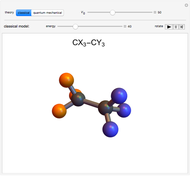
,  ; (4) hydrogen-like radial function with
; (4) hydrogen-like radial function with  ,
,  ,
,  ,
,  .
.
Contributed by: S. M. Blinder (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
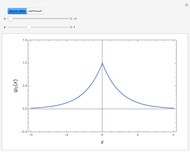
The closure relation can be derived by considering the expansion of an arbitrary function  obeying the same analytic and boundary conditions as the eigenfunctions
obeying the same analytic and boundary conditions as the eigenfunctions  . If the set of eigenfunctions is complete, one can write
. If the set of eigenfunctions is complete, one can write  , with expansion coefficients determined from
, with expansion coefficients determined from  . Substituting the last relation into the expansion, we find
. Substituting the last relation into the expansion, we find  , with the summation equivalent to the delta function
, with the summation equivalent to the delta function  .
.
Reference: Any graduate-level text on quantum mechanics.
Permanent Citation