Details

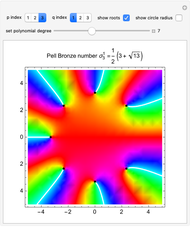
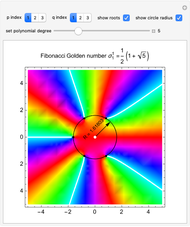
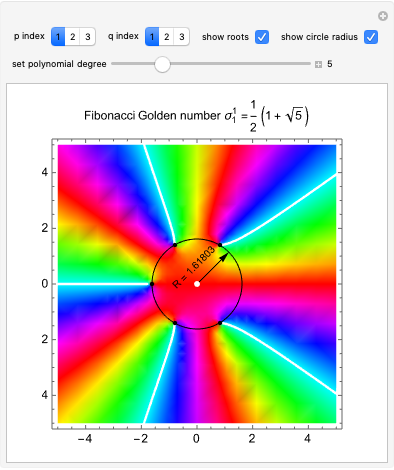
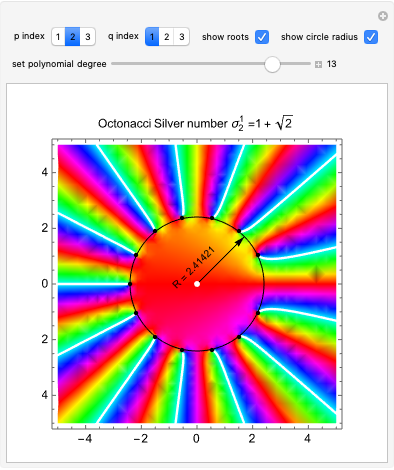
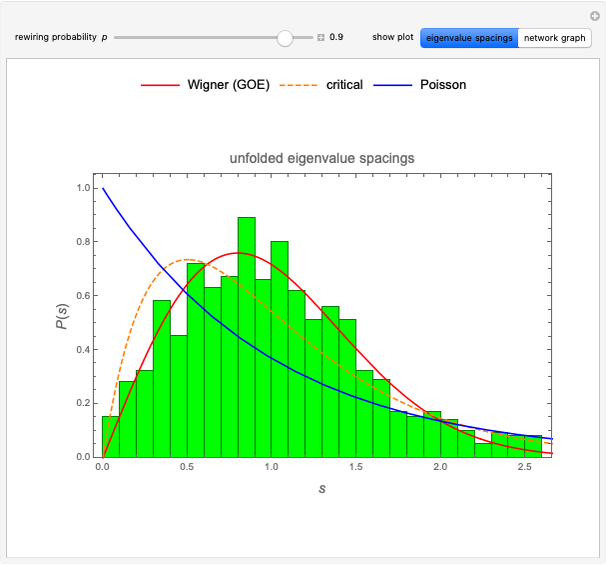
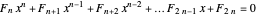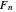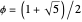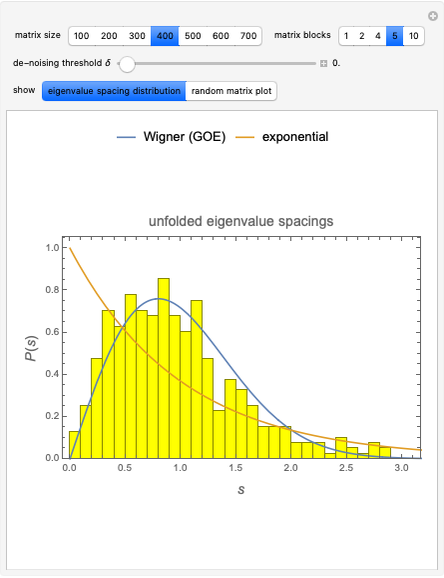
This Demonstration shows a generalization to other "metallic" numbers beyond the golden ratio of S. Rabinowitz's result for the complex roots of polynomials with coefficients from the Fibonacci sequence. According to his statements in [1, 2], each root of the equation , with each being a Fibonacci number, has absolute value near , the golden ratio. 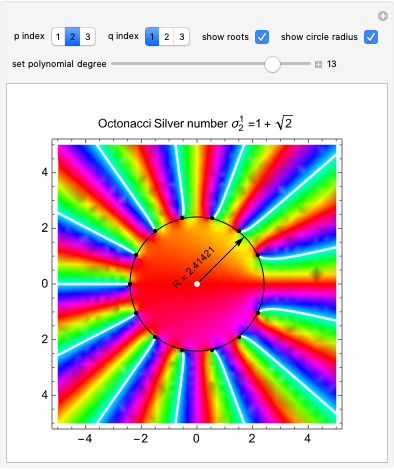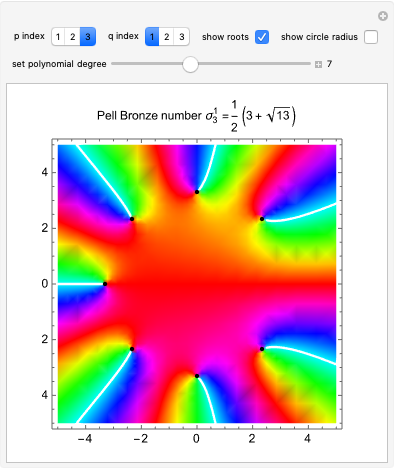This Demonstration shows that by introducing polynomial coefficients from generalized Fibonacci sequences with integers (see [3]), each root of the corresponding equation has an absolute value near the corresponding metallic number 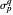. From a geometrical standpoint, this implies that the polynomial roots all lie on a circle of radius 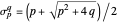. For example, for 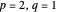it can be seen that the ratio of consecutive terms 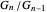tends to the silver mean 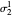. Thus, the polynomial zeros are found on a corresponding circle of radius 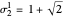. 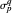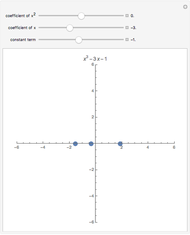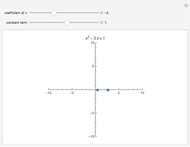Use the interactive controls to visually explore the results for different metallic numbers by changing the values of the corresponding 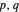setters. Use the "set polynomial degree" slider to change the polynomial degree, and therefore the number of complex roots from 3 up to 15. The provided checkboxes allow for the superposition of the circle and the corresponding root points with annotated radius This work was inspired by a Wolfram community post related to Rabinowitz's problem (see Related Links).

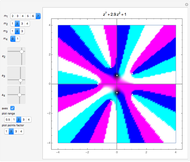
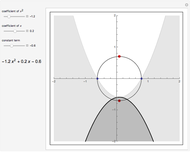
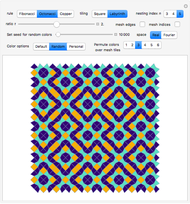
Snapshot 1: complex plot of roots of the 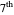degree polynomial for the bronze number generalized sequence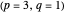

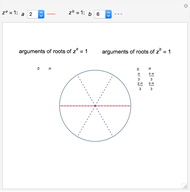
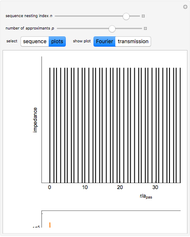
Snapshot 2: complex plot for the degree polynomial for the Fibonacci sequence with highlighted circle of radius equal to the golden number

Snapshot 3: complex plot for the degree polynomial for the generalized Fibonacci sequence 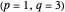with highlighted circle of radius equal to the nickel number

References

[1] R. E. Whitney, ed., "Advanced Problems and Solutions," The Fibonacci Quarterly, 26(3), 1988 pp. 283–288. (Jun 16, 2021) www.fq.math.ca/Scanned/26-3/advanced26-3.pdf.

[2] R. E. Whitney, ed., "Advanced Problems and Solutions," The Fibonacci Quarterly, 28(3), 1990 pp. 283–288. (Jun 16, 2021) www.fq.math.ca/Scanned/28-3/advanced28-3-a.pdf.

[3] V. W. De Spinadel, "The Metallic Means Family and Art," Journal of Applied Mathematics, 3(1), 2010 pp. 53–64. (Jun 16, 2021) www.aplimat.com/files/Journal_volume_3/Number_1.pdf.