Composition and Transformations

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
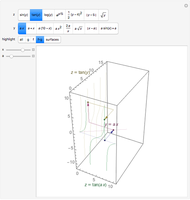
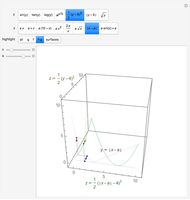
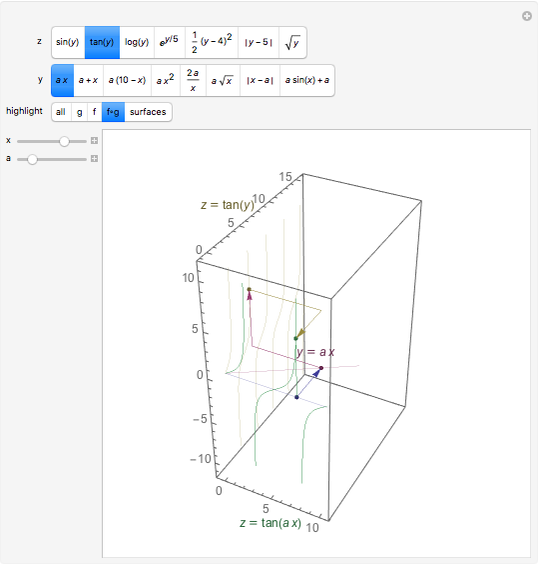
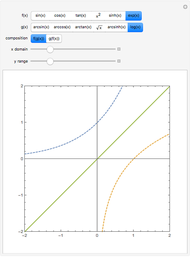
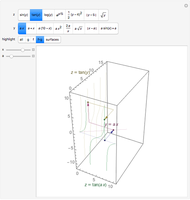
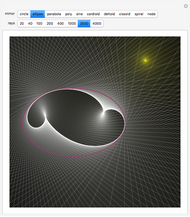
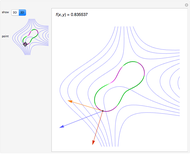
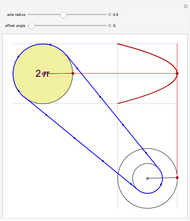
One way to visualize composition is to decompose 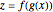 into
into  and
and 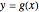 and plot the graph of each in its respective coordinate planes. You can then follow the arrows: Plug
and plot the graph of each in its respective coordinate planes. You can then follow the arrows: Plug  into
into 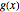 to get
to get  ; then plug
; then plug  into
into  to get
to get  ; and finally match up
; and finally match up  and
and  to get a point on
to get a point on 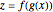 . The inside function
. The inside function 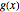 depends on a parameter
depends on a parameter  , which may be changed. Equivalently, this construction is the projection onto the
, which may be changed. Equivalently, this construction is the projection onto the  -
- plane of the intersection of the surfaces
plane of the intersection of the surfaces  and
and 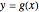 .
.
Contributed by: Michael Rogers (March 2011)
(Oxford College of Emory University)
Open content licensed under CC BY-NC-SA
Snapshots
Details
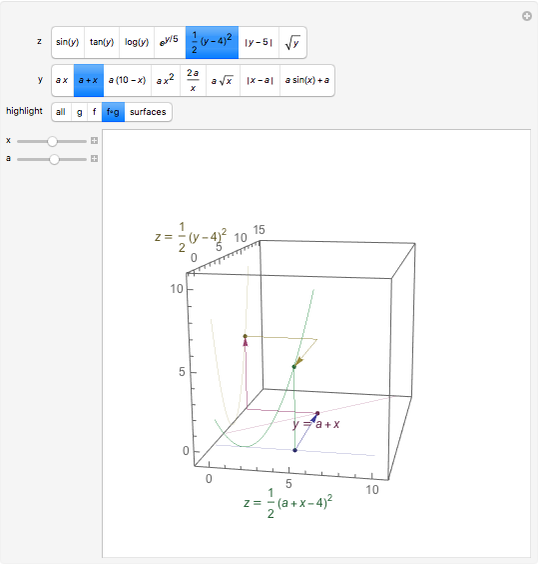
Choose functions for 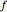 and
and  . The first two choices for
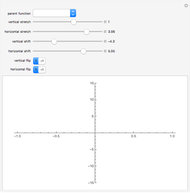
. The first two choices for  scale and translate the graph of
scale and translate the graph of 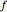 . The third incorporates a reflection. The rest transform the graph of
. The third incorporates a reflection. The rest transform the graph of 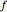 in complicated ways. Alternately, the outside function
in complicated ways. Alternately, the outside function 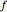 may be viewed as transforming the graph of
may be viewed as transforming the graph of  . The choices for
. The choices for 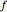 and
and  were selected because of their fundamental nature. In some cases they are scaled or translated for the sake of presentation. While the focus of this Demonstration is composition, studying the composition of these functions is a good way to improve your understanding of these functions.
were selected because of their fundamental nature. In some cases they are scaled or translated for the sake of presentation. While the focus of this Demonstration is composition, studying the composition of these functions is a good way to improve your understanding of these functions.
Sliding  shows how the values of
shows how the values of 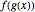 are determined from the values of
are determined from the values of  and
and 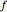 . Sliding
. Sliding  show how the transformation of the graph of
show how the transformation of the graph of 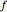 changes. This can be helpful for understanding the simple transformations studied in precalculus (the first three choices for
changes. This can be helpful for understanding the simple transformations studied in precalculus (the first three choices for  ). Highlight "surfaces" to show the intersection of
). Highlight "surfaces" to show the intersection of  and
and 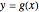 .
.
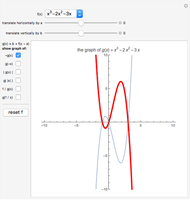
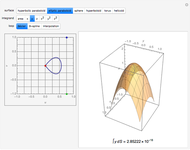
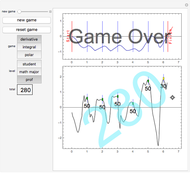
Snapshot 1: a scaling—the period of the tangent is stretched
Snapshot 2: a translation—the vertex of the parabola is shifted from  toward the origin
toward the origin
Snapshot 3: the effect of substituting an absolute value into a function—a mirror image about the vertex of the graph of the absolute value
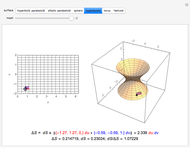
Snapshot 4: the effect of substituting into the absolute value function—the part of the graph below the  axis is reflected over the
axis is reflected over the  axis
axis
Snapshot 5: the important example from calculus,  —looks better with larger values of
—looks better with larger values of 
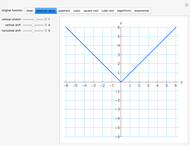
Snapshot 6: the square root of a function whose graph is tangent to the  axis (contact order exactly 1) has a "V" like the absolute value
axis (contact order exactly 1) has a "V" like the absolute value
Permanent Citation