Surface Parametrizations and Their Jacobians

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
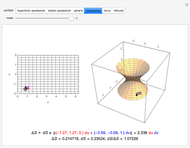
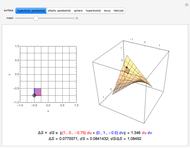
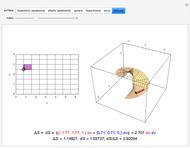
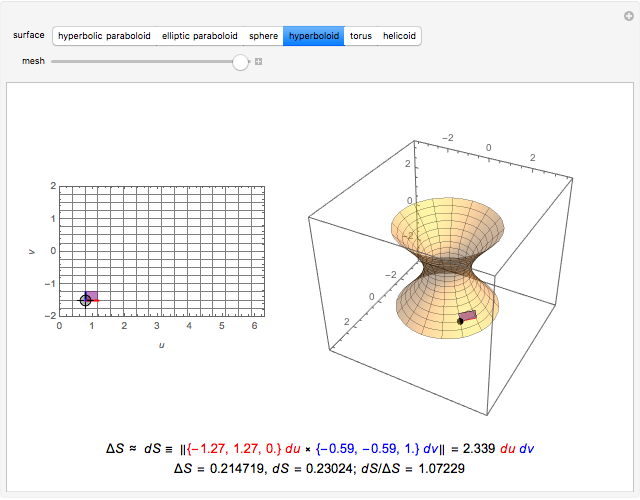
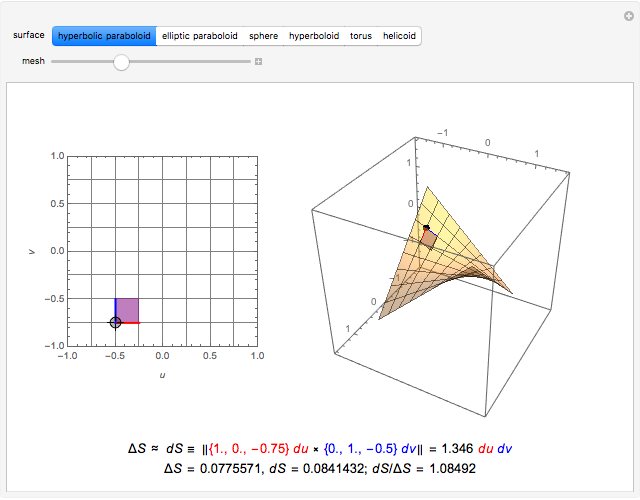
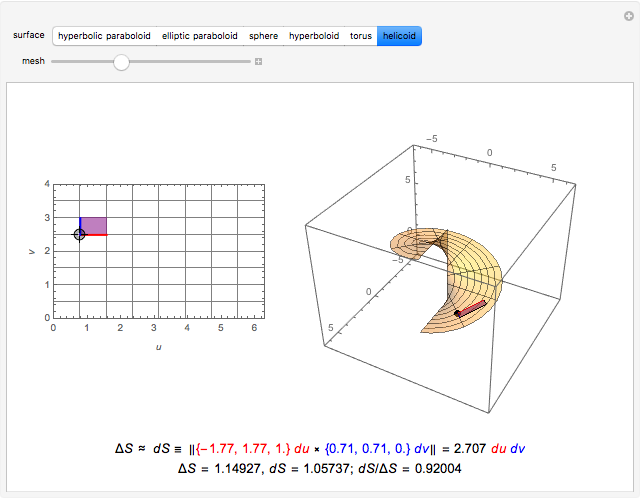
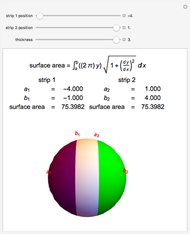
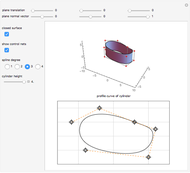
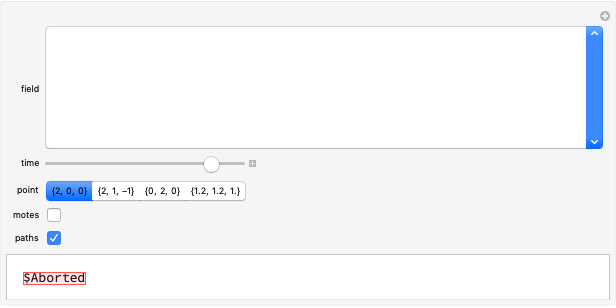
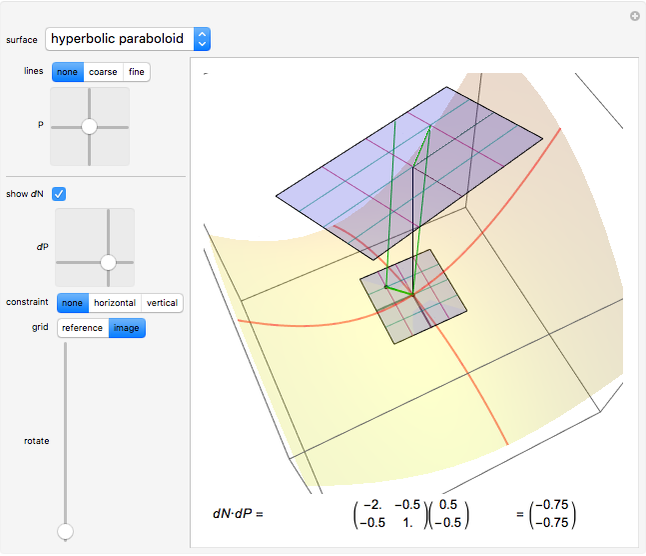
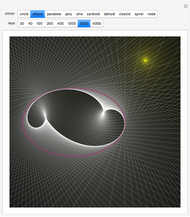
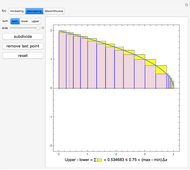
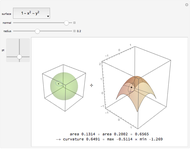
Given a parametrized surface, a little rectangle 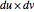 in the domain of the parametrization
in the domain of the parametrization  maps onto a segment of the surface. Approximate the area
maps onto a segment of the surface. Approximate the area 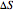 of the segment by the area
of the segment by the area 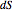 of a parallelogram spanned by tangent vectors given by
of a parallelogram spanned by tangent vectors given by 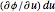 and
and 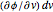 . The area of the parallelogram is equal to a factor
. The area of the parallelogram is equal to a factor 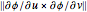 times the area
times the area 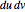 of the rectangle. The local scaling factor
of the rectangle. The local scaling factor 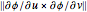 is sometimes called the Jacobian of the parametrization. As the base
is sometimes called the Jacobian of the parametrization. As the base 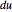 and height
and height 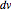 diminish (making the mesh finer), the ratio of the area of the parallelogram in the range to the corresponding area of the rectangle in the domain approaches the value of the Jacobian. Equivalently, the ratio of the areas of the segment of the surface and of the parallelogram approaches 1.
diminish (making the mesh finer), the ratio of the area of the parallelogram in the range to the corresponding area of the rectangle in the domain approaches the value of the Jacobian. Equivalently, the ratio of the areas of the segment of the surface and of the parallelogram approaches 1.
Contributed by: Michael Rogers (March 2011)
(Oxford College of Emory University)
Open content licensed under CC BY-NC-SA
Snapshots
Details
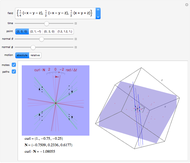
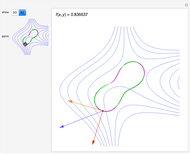
You can drag the point in the domain. The red segment of length 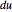 in the domain is mapped to the red tangent vector
in the domain is mapped to the red tangent vector 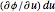 . Similarly, the blue segment of length
. Similarly, the blue segment of length 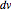 in the domain is mapped to the blue tangent vector
in the domain is mapped to the blue tangent vector 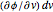 .
.
The concept illustrated in this Demonstration is key to understanding and defining surface area and surface integrals. See, for instance, the MathWorld link to surface integrals below, in which 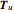 corresponds to
corresponds to 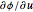 and
and 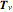 to
to 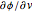 .
.
Permanent Citation