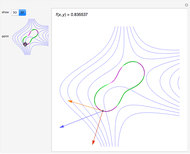
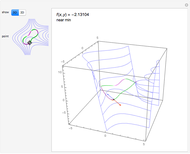
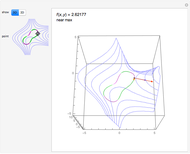
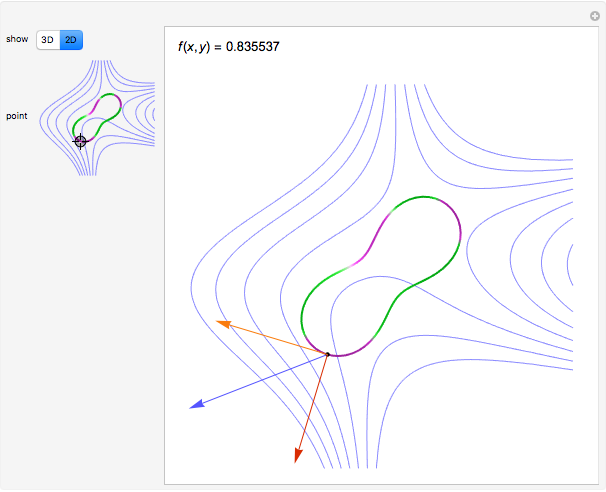
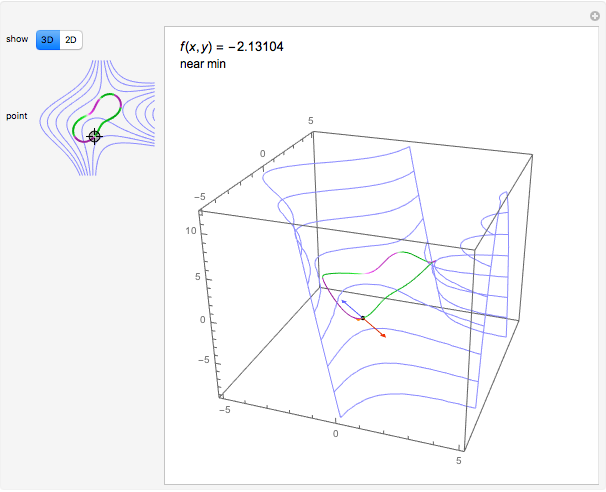
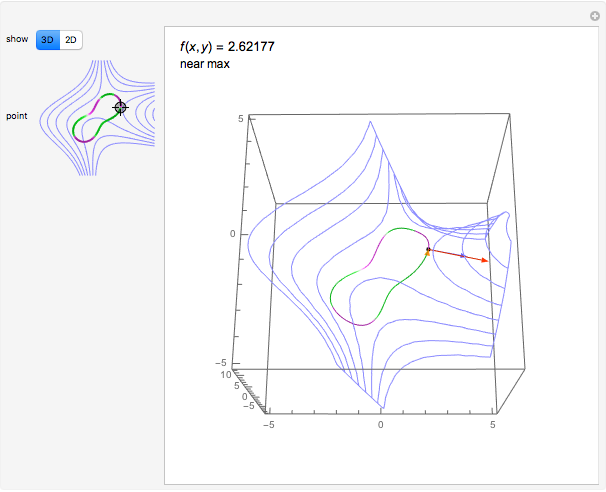
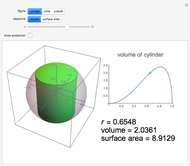
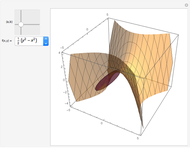
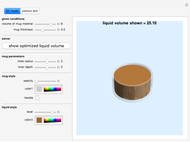
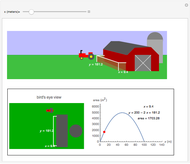
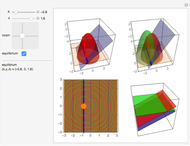
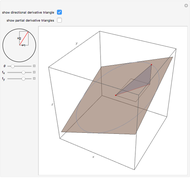
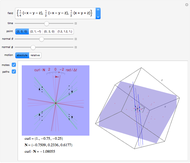
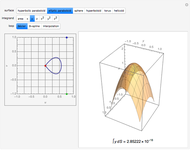
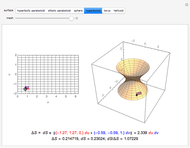
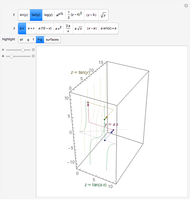
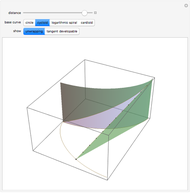
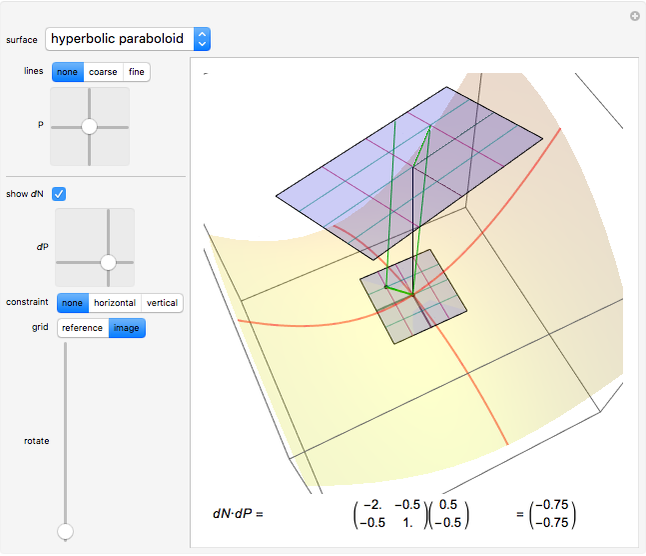
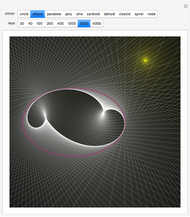
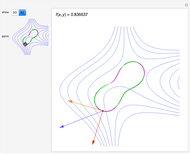
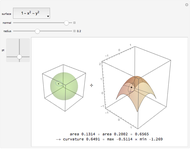
Move a point around a constraint curve to see the relationship between the blue gradient of the function
to be optimized and the red gradient of the function
for the constraint
. The orange vector is the projection of the gradient of
onto the tangent line of the constraint curve; its direction is the direction of increase along the constraint and its magnitude is the slope (that is, the directional derivative) of
in that direction. There are both 2D and 3D views, with the constraint curve laid out upon the graph of the function.
At a local extremum, the gradients of the functions
and
are parallel. Thus we get the condition for an extremum
, where
is called a Lagrange multiplier.
Browse all topics
