Swirl and the Curl

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
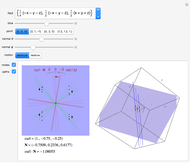
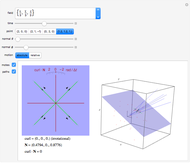
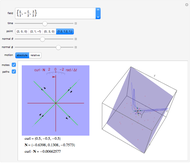
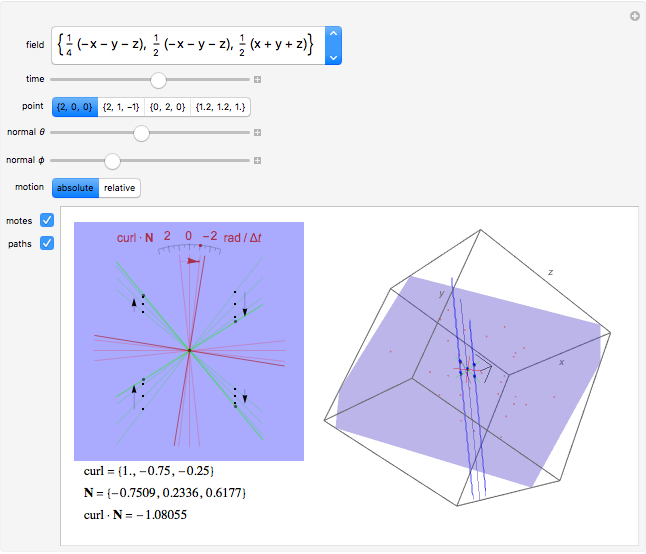
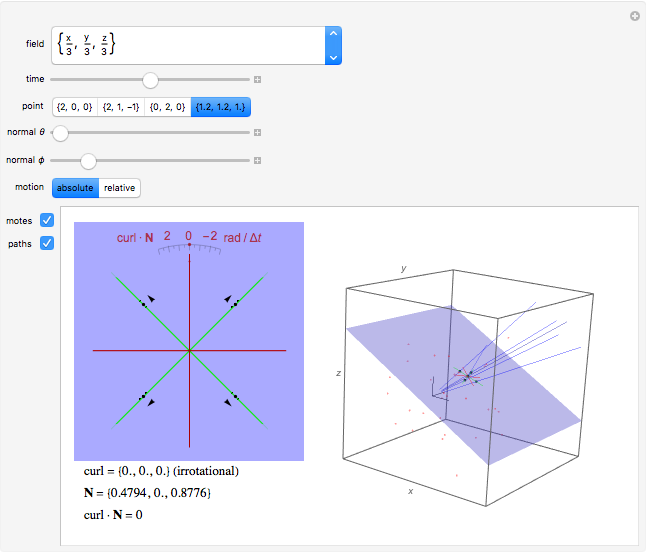
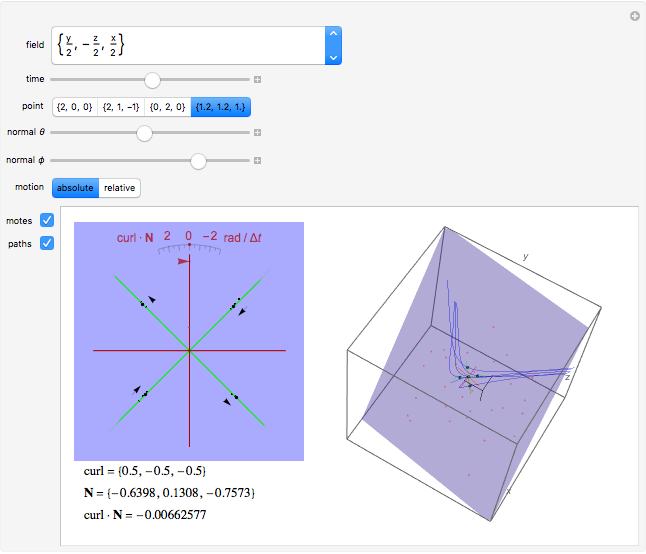
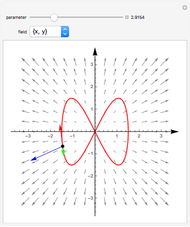
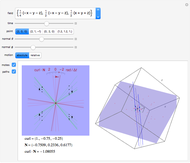
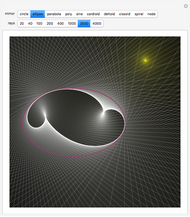
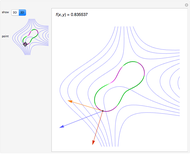
Imagine a moving fluid, such as air or water. Each point has a velocity vector, so that all the points make what is called a vector field. At each point in the flow, the curl of the vector field indicates the magnitude and orientation of the swirling of the flow. The curl can be visualized as follows. Near a given point, let there be a given plane containing the point and four nearby points that form a square cross in the plane. As time changes, the five points move out of the plane; let their "shadows" be projected orthogonally onto the plane, and let green lines join opposite points of the projected cross. Finally, let red lines bisecting the angles formed by the green lines be drawn in the plane. As time changes, the green lines move and the red bisectors rotate. The rotation of the red lines indicates the component of the curl in the direction normal to the plane. A succession of three such configurations of green and red lines is drawn on the left and forms a sort of scale; the rotation of the configuration is illustrated as it passes the selected point.
Contributed by: Michael Rogers (March 2011)
(Oxford College of Emory University)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The curl points in the direction about which there is maximum swirling. By Stokes' theorem, the curl at a point is equal to the limit of the circulation of the vector field about a loop divided by the area it encloses as the loop shrinks to the point. In the "paddle-wheel" model of this Demonstration, the normal component is equal to twice the angular rate of rotation (in radians per unit time) of the red cross.
Select one of the points to study. For reference, a coordinate trihedron is drawn at the origin. Adjust the spherical coordinates  and
and  of the normal to the plane. As the time moves through the center of the slider, the figure moves through the selected point, and you may observe the movement of the green lines and rotation of the red lines.
of the normal to the plane. As the time moves through the center of the slider, the figure moves through the selected point, and you may observe the movement of the green lines and rotation of the red lines.
On the motion displayed: Select "absolute" to see the actual movement. Select "relative" to see the motion relative to the velocity given by the vector field at the given point. Since the curl is a kind of derivative, it does not change if a constant vector is added or subtracted from the vector field. By subtracting the velocity vector at the selected point, we remove the translational component of the paddle wheel at the selected point so that the paddle wheel instantaneously has only a rotational component. This makes it easier to observe the swirling indicated by the curl. This affects only the three-dimensional graphics displayed.
The vector fields: The first six vector fields are linear. They have a constant curl, although the flow can look different at different points. The first three, 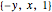 ,
, 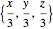 , and
, and 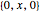 , are basic, linear fields: (1) the composition of a rotation about the
, are basic, linear fields: (1) the composition of a rotation about the  axis and a translation along the
axis and a translation along the  axis, (2) an expansion, and (3) a shear motion. The next three,
axis, (2) an expansion, and (3) a shear motion. The next three, 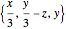 ,
, 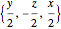 , and
, and 
 are slightly more complicated linear fields. It is particularly interesting that in the shear flows, the flow lines are straight even though the curl is nonzero. The last two vector fields are nonlinear. The first,
are slightly more complicated linear fields. It is particularly interesting that in the shear flows, the flow lines are straight even though the curl is nonzero. The last two vector fields are nonlinear. The first, 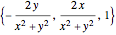 , has zero curl throughout its domain, and the next,
, has zero curl throughout its domain, and the next,  , has a curl opposite to the direction of rotation of the flow about the
, has a curl opposite to the direction of rotation of the flow about the  axis. These and the shear motions illustrate how flow paths might curve independently of the curl of the vector field.
axis. These and the shear motions illustrate how flow paths might curve independently of the curl of the vector field.
A note on the difference between the instantaneous curl and the average rate of swirling over a finite time: Notice that the green lines do not always pass through the opposite points as described in the caption above. In fact, they are drawn through the central point parallel to the lines joining the opposite points. The divergence of the points and the lines depends on the second derivatives of the components of the vector field and is negligible as the difference in time vanishes. It also depends on how close the points are to the central point. In the case of a linear field, the coincidence of the points and the lines is perfect, since the second derivatives are zero.
Permanent Citation