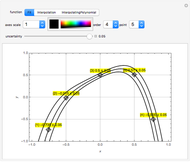
Concentrations of Multiple Reacting Species in a Semi-Infinite Region

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
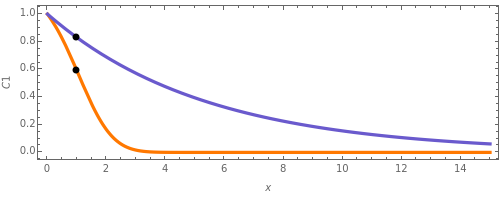
A new matrix method is demonstrated for the solution of partial differential equations coupled with first-order reactions representing multi-species reactive transport. In contrast to existing methods, the coupling matrix can have multiple eigenvalues.
[more]
Contributed by: Mikhail Dimitrov Mikhailov (INMETRO, Brazil) (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
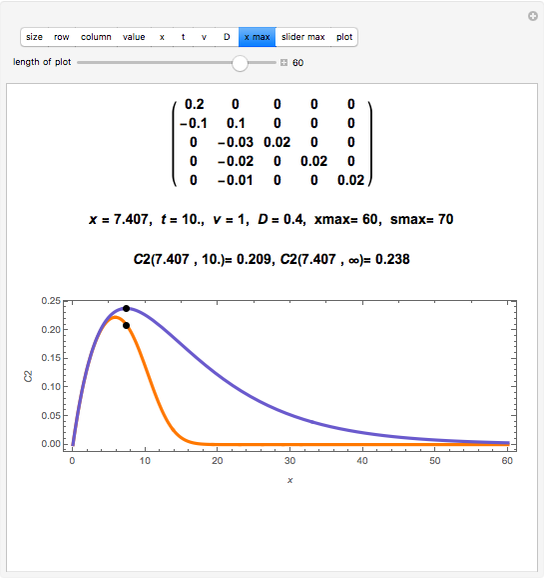
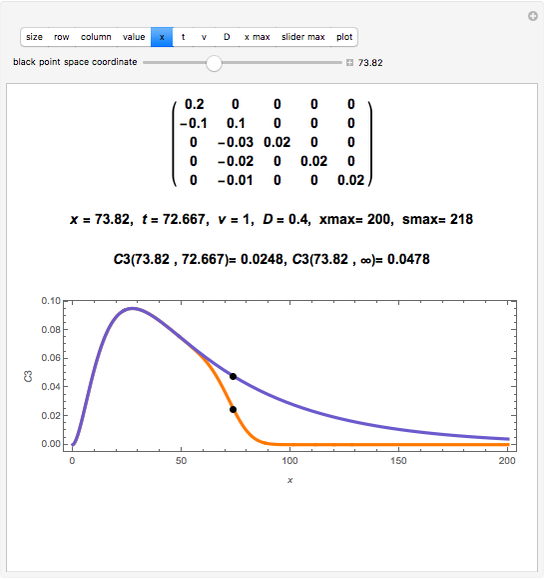
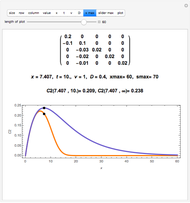
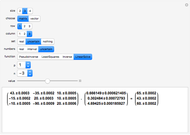
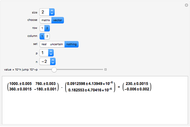
The classical multi-species reactive transport model can be written in matrix form as
 ,
,
where  is a species concentration vector in units of
is a species concentration vector in units of 
 ,
,  is a dimensionless surface concentration vector with first element
is a dimensionless surface concentration vector with first element  and the other elements
and the other elements  ,
, 
 is a space coordinate,
is a space coordinate,  is time,
is time,  is the flow velocity,
is the flow velocity,  is the hydrodynamic dispersion coefficient, and
is the hydrodynamic dispersion coefficient, and 
 is a matrix formed by contaminant destruction rates and dimensionless stoichiometric yield factors.
is a matrix formed by contaminant destruction rates and dimensionless stoichiometric yield factors.
Such models are of vital importance for evaluating the distribution of decaying radionuclides via several intermediates in the subsurface environment, contamination of aquifers with reactive substances, etc. The most important papers are those of Quezda, et al. [1].
It is surprising that in the 20th century no one solved the multi-species reactive transport problem by using the well-known similarity transformation technique [2]. It seems that Clement [3] was the first to apply the similarity transformation to multi-species equations. "...this solution method is feasible only when the first-order rate constants of the transported species have different numerical values [3]"—that is, the coupling matrix has distinct eigenvalues.
The modified rules from [4] applied to  , where only
, where only  is a matrix, directly give the desired solutions as linear combinations of the one-dimensional analytical solutions given in [5], in which instead of
is a matrix, directly give the desired solutions as linear combinations of the one-dimensional analytical solutions given in [5], in which instead of  the eigenvalues of the matrix
the eigenvalues of the matrix  appeared.
appeared.
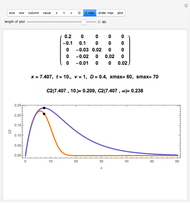
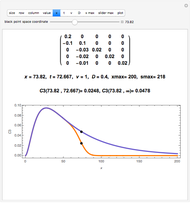
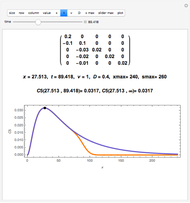
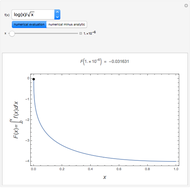
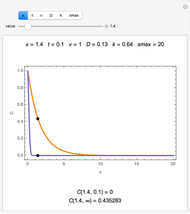
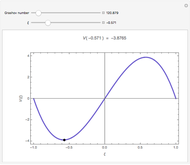
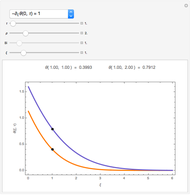
Since the initial settings correspond to the one from [6, p. 188, Table 1], the parameters in the original plots can be modified to see their effects.
This Demonstration can plot only the distributions of concentrations in infinite half-space with a fixed concentration at the boundary surface, but the developed matrix method is applicable for a large class of models, including different boundary conditions and space dimensions.
[1] C. R. Quezada, T. P. Clement, and K. K. Lee, "Generalized Solution to Multi-Dimensional Multi-Species Transport Equations Coupled with a First-Order Reaction Network Involving Distinct Retardation Factors," Advances in Water Resources, 27, 2004 pp. 507–520.
[2] M. D. Mikhailov and M. N. Ozisik, "On the Decoupling of a System of Diffusion Equations," J. Appl. Phys, 63, 1988 pp. 972–973.
[3] T. P. Clement, "Generalized Solution to Multispecies Transport Equations Coupled with a First Order Network," Water Resources Research, 37, 2001 pp. 157–163.
[4] M. D. Mikhailov, "Functions of Matrices," The Wolfram Demonstrations Project.
[5] M. D. Mikhailov, "Convection-Diffusion in a Semi-Infinite Region," The Wolfram Demonstrations Project.
[6] Y. Sun, J. N. Petersen, T. P. Clement, and R. S. Skeen, "Development of Analytical Solutions for Multispecies Transport with Serial and Parallel Reactions," Water Resources Research, 359, 1999 pp. 185–190.
Permanent Citation