Uncertain Calculus: Mean versus Likelihood Mean

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
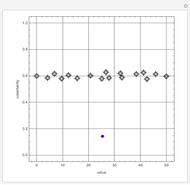
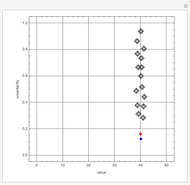
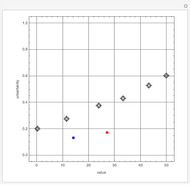
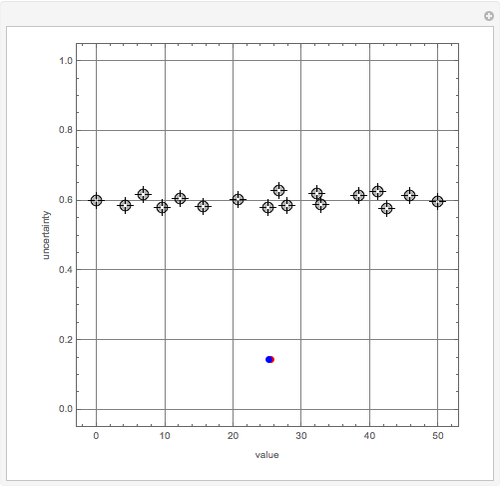
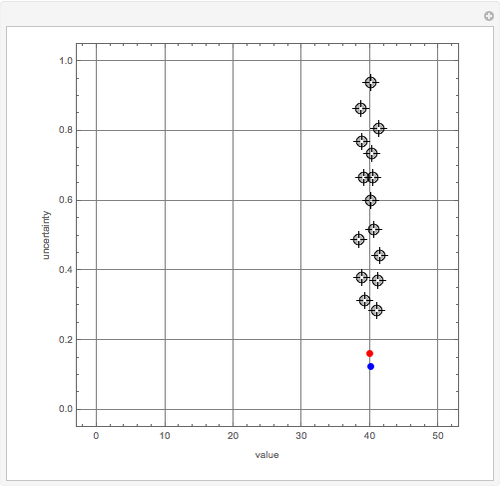
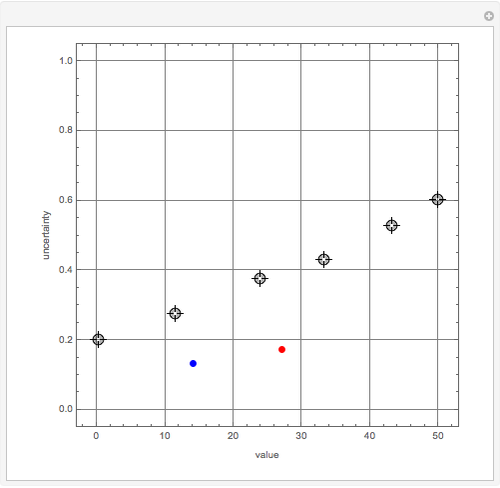
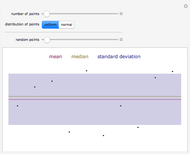
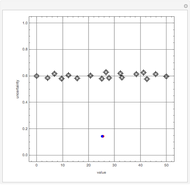
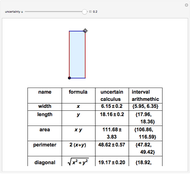
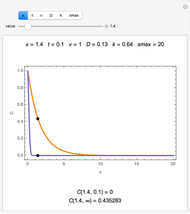
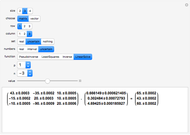
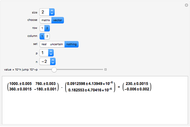
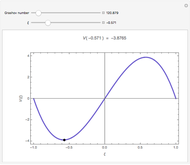
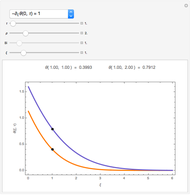
This Demonstration visualizes the mean of  measurements of the same quantity made by different methods, different laboratories, or different instruments. The measurements are given in the form of uncertain numbers
measurements of the same quantity made by different methods, different laboratories, or different instruments. The measurements are given in the form of uncertain numbers  , plotted as locators with coordinates
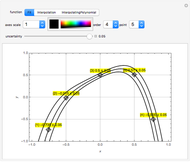
, plotted as locators with coordinates  . The red point gives the mean of all the points calculated by the uncertain calculus, while the mean of the blue points is computed by the likelihood method.
. The red point gives the mean of all the points calculated by the uncertain calculus, while the mean of the blue points is computed by the likelihood method.
Contributed by: Valter Yoshihiko Aibe and Mikhail Dimitrov Mikhailov (INMETRO, Brazil) (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
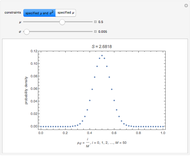
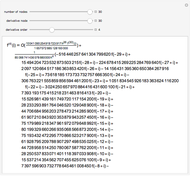
The uncertain calculus was introduced in [1] and explored in previous Demonstrations (see the Related Links). The uncertain calculus gives the formula implemented as the uncertainCalculusMean function, which computes the mean of the uncertain numbers defined by the locators and shown as a red point.
The likelihood method formulas are given in [2], eqs. 11.14 and 11.19, and Maximum Likelihood (Wolfram MathWorld), eqs. 19 and 24. These expressions and special cases are implemented as the likelihoodMean function that computes the coordinates of the blue point.
References:
[1] V. Y. Aibe and M. D. Mikhailov, "Uncertainty Calculus in Metrology," Proceedings of ENCIT 2008, 12th Brazilian Congress of Thermal Engineering and Sciences, Belo Horizonte, MG, Brazil, November 10–14, 2008.
[2] José Henrique Vuolo, Fundamentos da Teoria de Erros, 2nd ed., 2nd printing, Sao Paulo, Brazil: Edgar Blucher, LTDA, 2000.
Permanent Citation
"Uncertain Calculus: Mean versus Likelihood Mean"
http://demonstrations.wolfram.com/UncertainCalculusMeanVersusLikelihoodMean/
Wolfram Demonstrations Project
Published: March 7 2011