Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Natural Convection between Two Vertical Plates

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

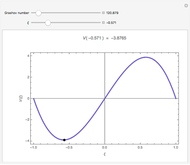
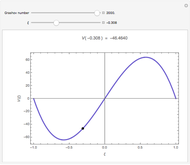
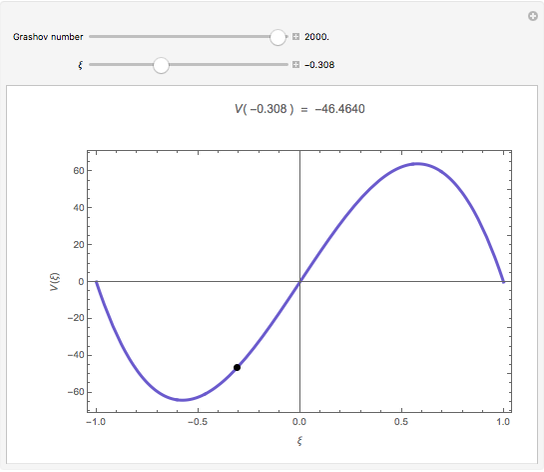
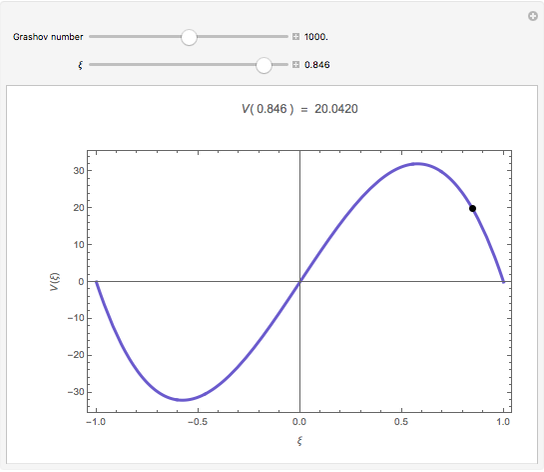
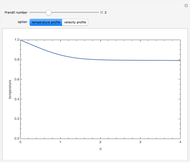
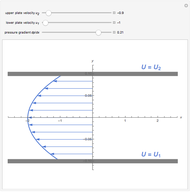
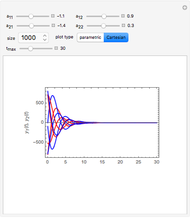
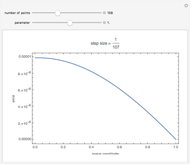
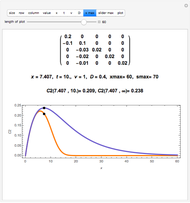
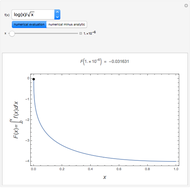
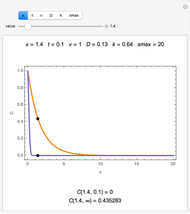
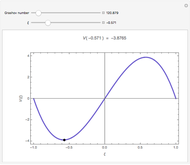
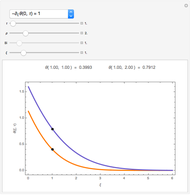
The dimensionless vertical velocity inside two vertical plates at distance and temperatures and is computed for specified Grashov number , where is the velocity , is the distance in meters, is the kinematic viscosity in , is the gravitational acceleration in , and is the volumetric coefficient of thermal expansion in.

[more]

For a fixed Grashov number, determines black points on the curve, followed by the numerical values of . Thus for any and the precise values of the velocity are available.

The frame ticks change with Grashov number , which conveniently lets you observe that the shape of the velocity distribution did not change.

[less]

Contributed by: Mikhail Dimitrov Mikhailov (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

$Failed
Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send