Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Drilling a Triangular Hole

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

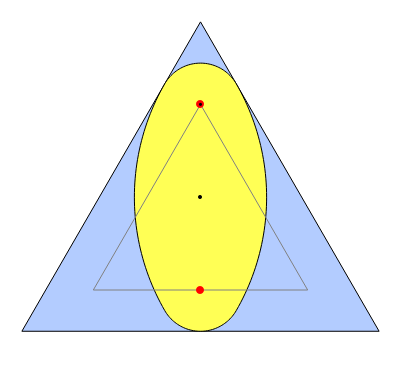
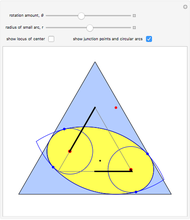
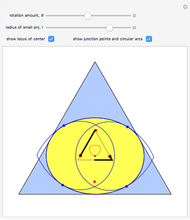
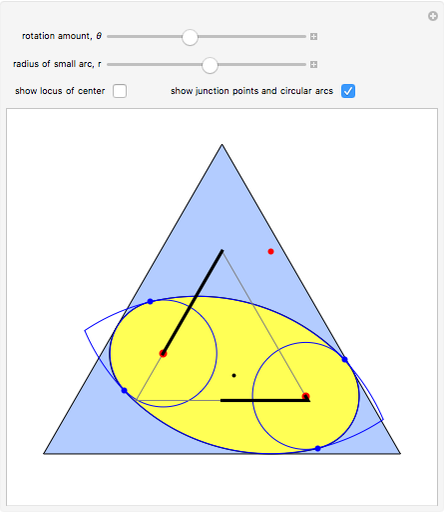
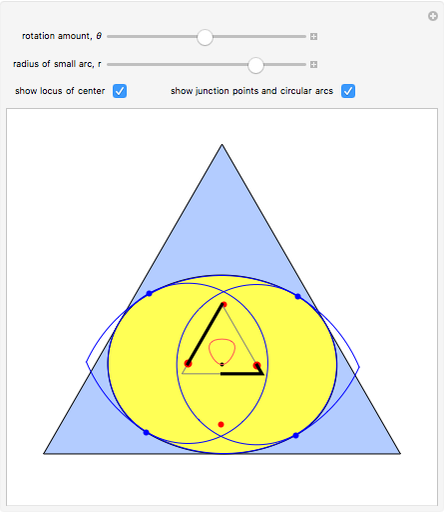
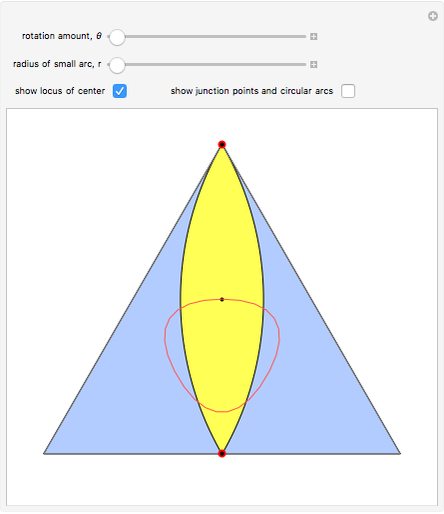
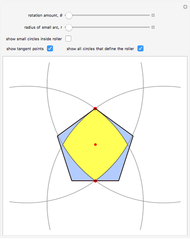
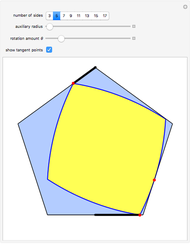
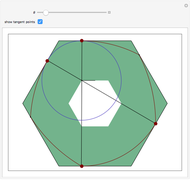
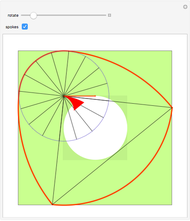
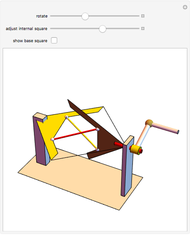
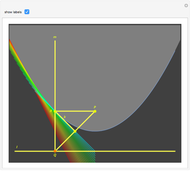
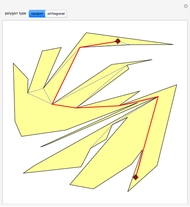
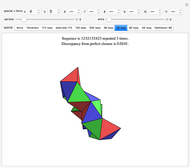
The construction shown allows you to turn circular motion into triangular motion and so construct a drill for triangular holes. The roller—the yellow shape that rotates inside the large triangle—consists of four circular arcs. As it rotates, the centers of the smaller circles trace out an exact equilateral triangle. You can vary the size of the roller so as to get triangular holes of different sizes without changing the ambient triangle.

Contributed by: Barry Cox (University of Wollongong) and Stan Wagon (Macalester College) (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

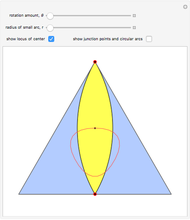
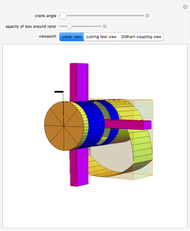
The existence of such a device was stated as an open question in [1]. To turn this geometrical construction into a working drill with a driving end that follows plain circular motion, one would use an Oldham coupling, as shown in the Demonstration "Square-Hole Drill in Three Dimensions". Snapshot 3 shows how the roller can become two-sided when the radius of the smaller circle is set to 0; in that case the locus of the cusp coincides with the ambient triangle.

[1] B. Cox and S. Wagon, "Mechanical Circle-Squaring," College Mathematics Journal, 40(4), 2009 pp. 238–247.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send