Drilling an n-Gon Hole for Odd n

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
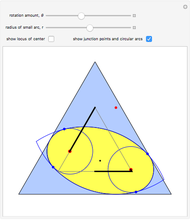
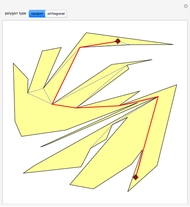
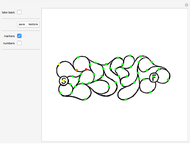
The construction shown turns circular motion into polygonal motion that drills polygonal holes, provided the polygon is regular and has an odd number of sides. The rotor—the yellow shape that rotates within the large  -gon—consists of
-gon—consists of  circular arcs. As it rotates, the two centers of the smaller circles trace out an exact regular
circular arcs. As it rotates, the two centers of the smaller circles trace out an exact regular  -gon. You can vary the size of the roller so as to get polygonal holes of different sizes without changing the ambient polygon.
-gon. You can vary the size of the roller so as to get polygonal holes of different sizes without changing the ambient polygon.
Contributed by: Barry Cox and Stan Wagon (University of Wollongong and Macalester College) (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
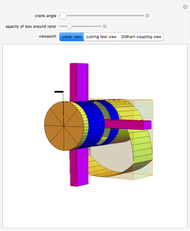
The existence of such a device was stated as an open question in [1]. To turn this geometrical construction into a working drill with a driving end that follows plain circular motion, you could use an Oldham coupling, as shown in the Demonstration "Square-Hole Drill in Three Dimensions".
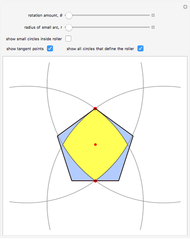
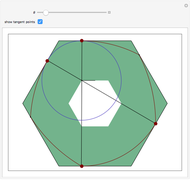
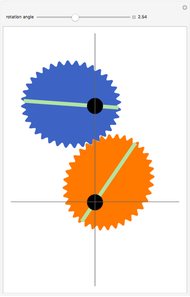
Snapshot 1: shows the case  and
and  ; then the roller becomes the intersection of two copies of a vesica pisces (a vesica pisces is the intersection of two congruent circles, where the center of each circle lies on the boundary of the other one—see the MathWorld entry for "Lens (Wolfram MathWorld)"); in this case, the locus of the cusp is identical to the ambient pentagon
; then the roller becomes the intersection of two copies of a vesica pisces (a vesica pisces is the intersection of two congruent circles, where the center of each circle lies on the boundary of the other one—see the MathWorld entry for "Lens (Wolfram MathWorld)"); in this case, the locus of the cusp is identical to the ambient pentagon
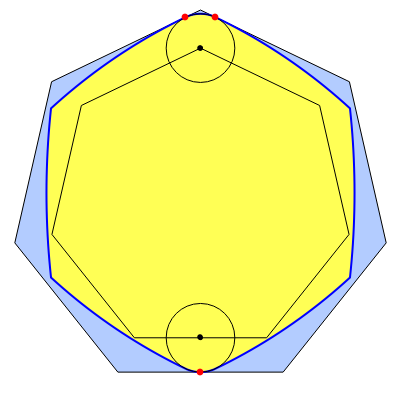
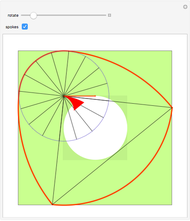
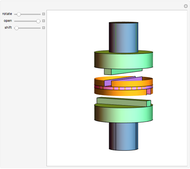
Snapshot 2: shows the case of a heptagon, with large  ; the locus is a rather small pentagon
; the locus is a rather small pentagon
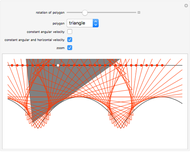
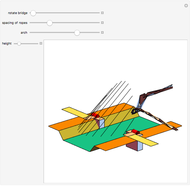
Snapshot 3: shows the case of an 11-sided polygon
The construction is based on an envelope construction similar to that in [1] to determine the proper centers and radii of the large circular arcs that define the rotor. It is critical that, for each orientation of the rotor, its position within the large polygon is determined. This holds true because there are always three tangency points, shown in red, and they prevent up-down or left-right motion. We do not yet have a general proof that there are always such tangent points, but we have verified it numerically for  .
.
For even-sided polygons, the square was solved in the 1930s and in [1] the authors dealt with the hexagonal case, which required some careful analysis. The construction in [1] has also been successfully applied to the octagon and the authors conjecture that similar ideas can be used for all even-sided polygons. However, this remains an unsolved problem.
Reference:
[1] B. Cox and S. Wagon, "Mechanical Circle-Squaring," College Mathematics Journal, 40(4), 2009 pp. 238–247.
Permanent Citation