Dynamics of Qubit Lattices

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
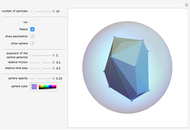
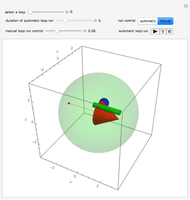
This Demonstration simulates the time evolution of a spin lattice (with spins 1/2, here also referred to as qubits) to show that parallel-aligned spins, in contrast to parallel-aligned classical magnetic dipoles, can form a dynamically stable state. As is customary for spin-lattice models, interaction between spins is restricted to the nearest neighbors. The interaction is given by a Heisenberg spin Hamiltonian with two parameters:  measuring the coupling to a homogeneous external magnetic field in the
measuring the coupling to a homogeneous external magnetic field in the  direction, and
direction, and  representing the spin-spin coupling, which for
representing the spin-spin coupling, which for 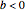 favors parallel spin alignment (ferromagnetic case).
favors parallel spin alignment (ferromagnetic case).
Contributed by: Ulrich Mutze (November 2018)
Open content licensed under CC BY-NC-SA
Details
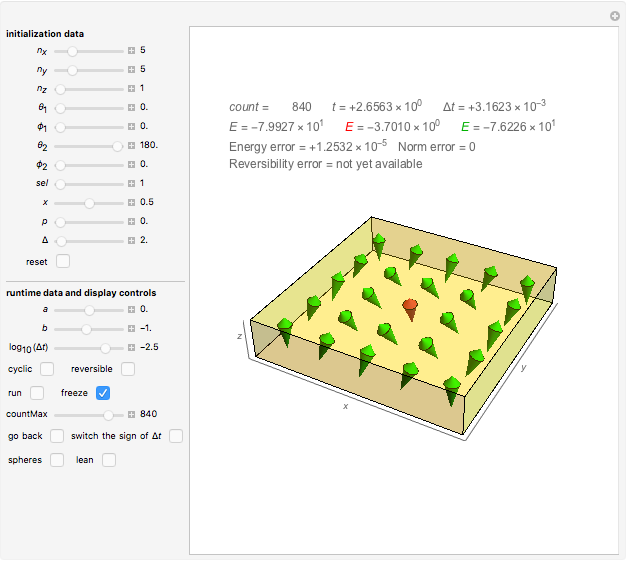
Use the "lean" box to toggle a label on the graphic to show some useful quantities. Play around with the initial conditions (i.e. the number of qubits, their partition into the green and red groups, the directions of the Bloch vectors and the boundary conditions) to learn why the three displayed energies have their indicated values. Insight into the behavior of qubits can be gained by running the configurations that are stored under the Bookmarks/Autorun menu.
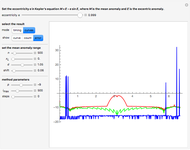
It turns out that in the long run, many configurations lead to exponentially exploding trajectories, if the time step is chosen large enough so that viewing the evolving graphics is not too boring. The tendency to become unstable depends strongly on the initial conditions, which is common in nonlinear integro-differential equations. For a general approach to the Hartree that fits the present framework, see [1, 2]. The integrators employed here are the methods DALF and ADALF in [3]. This Demonstration can be seen as a transformation of [4] from classical to quantum physics.
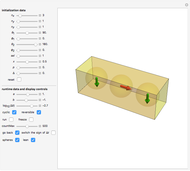
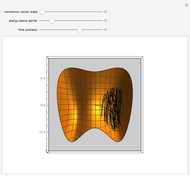
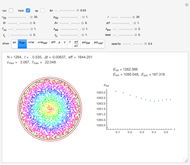
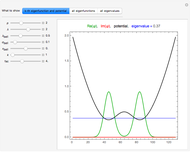
Snapshot 1: Initial state of aligned spins with the central spin reversed.
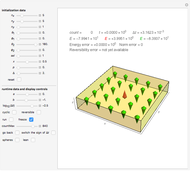
Snapshot 2: After 840 time steps, the central spin has turned to the majority direction and the other spins have turned slightly out of their ground-state positions. This is, in fact, a snapshot of an interesting dynamical process in which the central spin will return many times to states nearly as high in energy as the initial state. In the long run, we can observe something like equipartition of the energy over the spins. If we had built in a friction mechanism for degrading the energy that the central spin releases by swinging back to the majority direction, we would get a constant alignment over all spins. If we worked with more spins in a plane or even in 3D, we would come close to the constant alignment even without friction. What any program run with the initial conditions of Snapshot 1 shows convincingly is that the majority spins have a dynamically stable configuration in which the disturbance by the central spin causes only wiggling motions but no reorganization of the alignment.
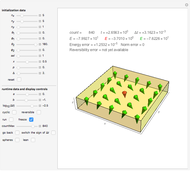
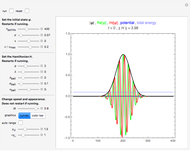
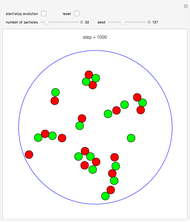
Snapshot 3: Evolved state from the initial state bookmarked as "two antiparallel chains." Signs of dynamical instability can be noted, that is, a tendency to change alignment locally.
Snapshot 4: Evolved state from the initial state bookmarked as "two parallel chains." No sign of dynamical instability is noticed, in accordance with our earlier observation on uniformly aligned spins.
References
[1] U. Mutze. "Separated Quantum Dynamics." (Nov 26, 2018) www.ma.utexas.edu/mp_arc/c/08/08-69.pdf.
[2] U. Mutze. "Quantum Image Dynamics—An Entertainment Application of Separated Quantum Dynamics." (Nov 26, 2008) www.ma.utexas.edu/mp_arc/c/08/08-199.pdf.
[3] U. Mutze, "An Asynchronous Leapfrog Method II." arxiv.org/abs/1311.6602.
[4] U. Mutze. "On the Ewing Model of Magnetism" from the Wolfram Demonstrations Project—A Wolfram Web Resource. demonstrations.wolfram.com/OnTheEwingModelOfMagnetism.
Snapshots
Permanent Citation