Monte Carlo Simulation of Two-Electron Spin Correlations

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
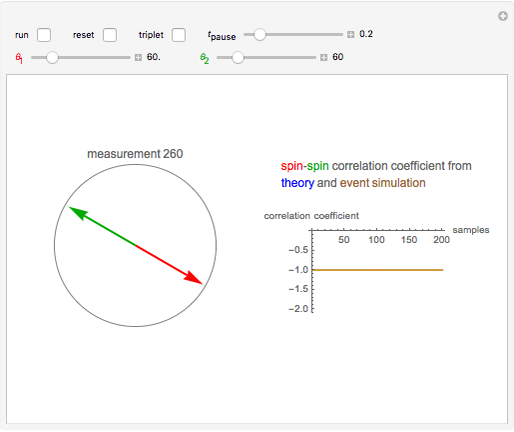
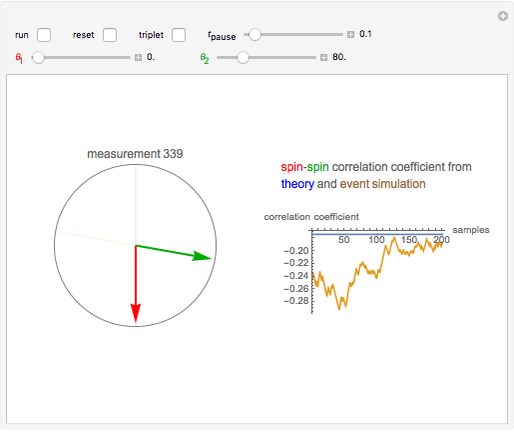
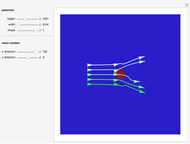
This Demonstration simulates the results of spin measurements on two-electron spins, using rotatable analyzers along directions  and
and  that can be selected by the user. The two electrons remain in an eigenstate of total spin squared.
that can be selected by the user. The two electrons remain in an eigenstate of total spin squared.
Contributed by: Ulrich Mutze (April 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
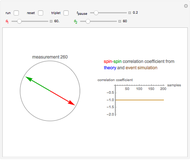
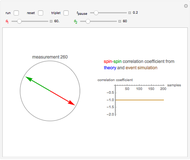
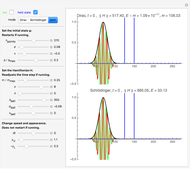
Snapshot 1: measuring along the same direction results in perfect anticorrelation
Snapshot 2: 10° deviation of the measuring directions allows parallel alignment in rare cases
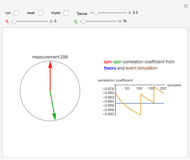
Snapshot 3: 10° deviation from orthogonality makes a small correlation coefficient
Snapshot 4: orthogonal directions make the correlation coefficient vanish
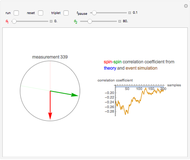
Snapshot 5: constructive addition of spins is the usual case in triplet states
This Demonstration considers the simplest nontrivial quantum system composed of two subsystems, allowing us to study the phenomenon of entanglement. This system was employed by D. Bohm in his discussion of the EPR "paradox" and is referred to in most discussions of Bell's inequality (see e.g. the Scholarpedia article "Bell's Theorem"). It is an idealized system in which the spacial dependence of the electron wavefunctions is ignored, and thus no (anti-)symmetry restrictions from Pauli's principle are imposed. Nevertheless, it turns out that the "groundstate" (i.e. the state with the lowest eigenvalue, 0 in this case) of the operator  , the so-called singlet state, is necessarily antisymmetric with respect to an exchange of the electrons. This state has the property that the spins, if both measured along the same direction (i.e.
, the so-called singlet state, is necessarily antisymmetric with respect to an exchange of the electrons. This state has the property that the spins, if both measured along the same direction (i.e.  ), are always found to be antiparallel.
), are always found to be antiparallel.
Permanent Citation