Standard Colorimetric Observer Color-Matching Functions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
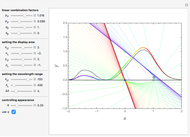
This Demonstration studies the functions of the form 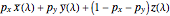 , where
, where  and
and 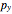 are real numbers and
are real numbers and  ,
,  ,
,  are the color-matching functions of the CIE 1931 Standard Colorimetric Observer. The main reason for being interested in these functions is that among them there are the spectral responses of electronic cameras that "see colors just like normal humans," meaning that two spectral distributions of radiant energy are indistinguishable for the camera if and only if they are indistinguishable for a normal human observer. Since spectral responses of photo detectors are always positive, the functions of interest are the positive ones. Since the
are the color-matching functions of the CIE 1931 Standard Colorimetric Observer. The main reason for being interested in these functions is that among them there are the spectral responses of electronic cameras that "see colors just like normal humans," meaning that two spectral distributions of radiant energy are indistinguishable for the camera if and only if they are indistinguishable for a normal human observer. Since spectral responses of photo detectors are always positive, the functions of interest are the positive ones. Since the  ,
,  ,
,  are positive by definition, trivially positive linear combinations result if
are positive by definition, trivially positive linear combinations result if  ,
, 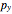 , and
, and  are positive. There are, however, also cases where one of these three coefficients is negative. These were determined in [1].
are positive. There are, however, also cases where one of these three coefficients is negative. These were determined in [1].
Contributed by: Ulrich Mutze (July 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
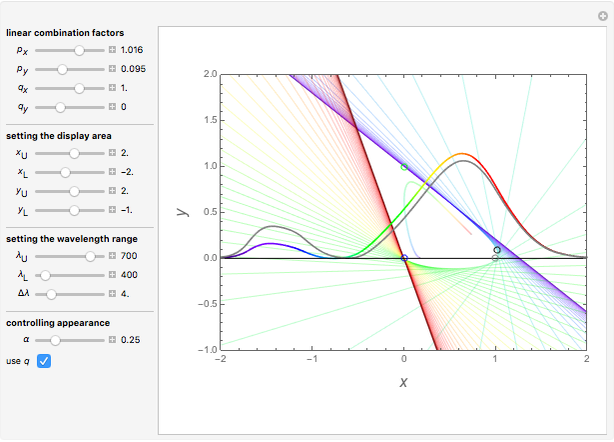
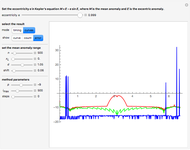
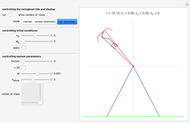
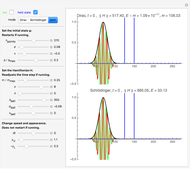
Snapshot 1: Best-concentrated red response (colored) and  for comparison (gray). The colored curve has a much smaller side lobe.
for comparison (gray). The colored curve has a much smaller side lobe.
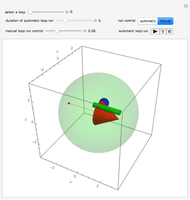
Snapshot 2: Best-concentrated red response (colored) and the best-concentrated red response without a side lobe (gray). The red-sensitive cones in the human eye have a spectral response similar to the gray curve.
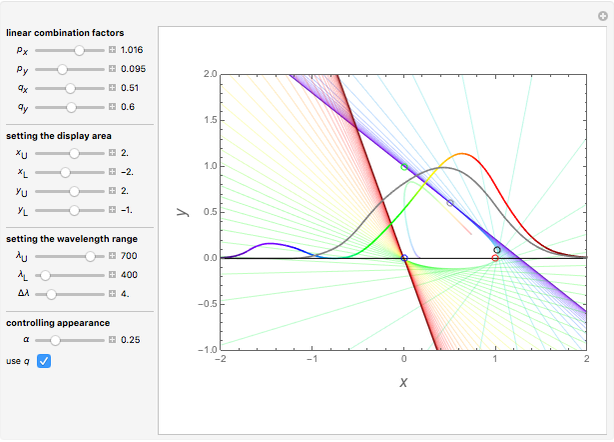
Snapshot 3: Best-concentrated green response (colored) and  for comparison (gray).
for comparison (gray).
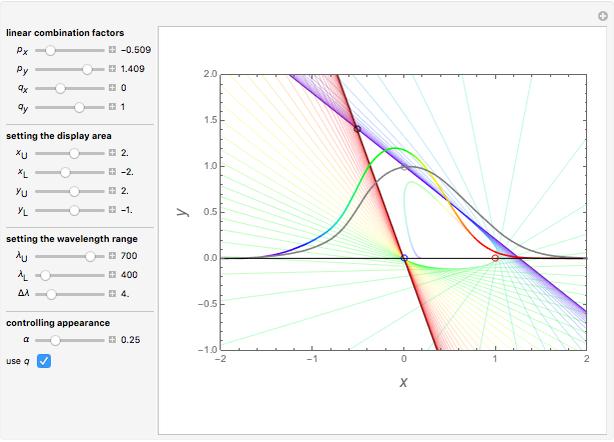
Snapshot 4: Best-concentrated blue response (colored) and  for comparison (gray). Since the two response curves differ only very little, only a small portion of the full display area is shown.
for comparison (gray). Since the two response curves differ only very little, only a small portion of the full display area is shown.
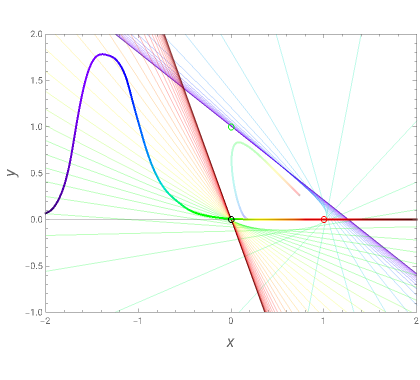
Among the positive functions of the form 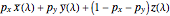 , there are members that show a stronger concentration toward a dominant wavelength than can be seen in the original functions
, there are members that show a stronger concentration toward a dominant wavelength than can be seen in the original functions  ,
,  ,
,  . Surprisingly, there is a well-defined triplet of best-concentrated functions. Their points
. Surprisingly, there is a well-defined triplet of best-concentrated functions. Their points  all belong to the boundary of the convex line-free area and are placed such that they form a triangle of maximal area. The particular geometry of the line-free area makes it easy to find these points: Two points are given as the two edges of the area and the third point is determined by having maximum distance from the connecting line between the two edges. If one poses the condition that each curve should have a single maximum, one has to choose the third point differently and finds that the area is 71% of the maximum area. Taking into account shot noise in the color channels of electronic cameras, one arrives at the conclusion that the number of distinguishable signal triplets is proportional to the triangle area [2].
all belong to the boundary of the convex line-free area and are placed such that they form a triangle of maximal area. The particular geometry of the line-free area makes it easy to find these points: Two points are given as the two edges of the area and the third point is determined by having maximum distance from the connecting line between the two edges. If one poses the condition that each curve should have a single maximum, one has to choose the third point differently and finds that the area is 71% of the maximum area. Taking into account shot noise in the color channels of electronic cameras, one arrives at the conclusion that the number of distinguishable signal triplets is proportional to the triangle area [2].
References
1. M. L. Pearson and J. A. C. Yule, "Transformations of Color Mixture Functions without Negative Portions," Journal of Color & Appearance, II(I), 1973.
2. U. Mutze, General Properties of Metamerism Preserving Color Imaging Systems, Kodak Technical Report, Hybrid Imaging Research Laboratories Europe, Accession No. 278861D 02/16/1993, unpublished.
Permanent Citation