On the Ewing Model of Magnetism

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
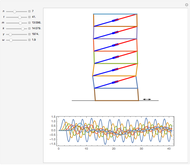
As the Scottish physicist James A. Ewing wrote near the end of the nineteenth century [1, p. 348]: "It is extremely helpful… to experiment with a model consisting of a number of short steel magnets pivoted like compass needles on fixed centers and placed near enough to one another to allow their mutual control to be felt." This Demonstration is a mathematical model of Ewing's device (for Ewing, a model was something that came out of a workshop). The main action is to activate the run box. Hover the pointer over the control labels to see tooltips with explanations.
Contributed by: Ulrich Mutze (July 2018)
Open content licensed under CC BY-NC-SA
Snapshots
Details
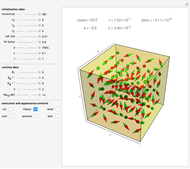
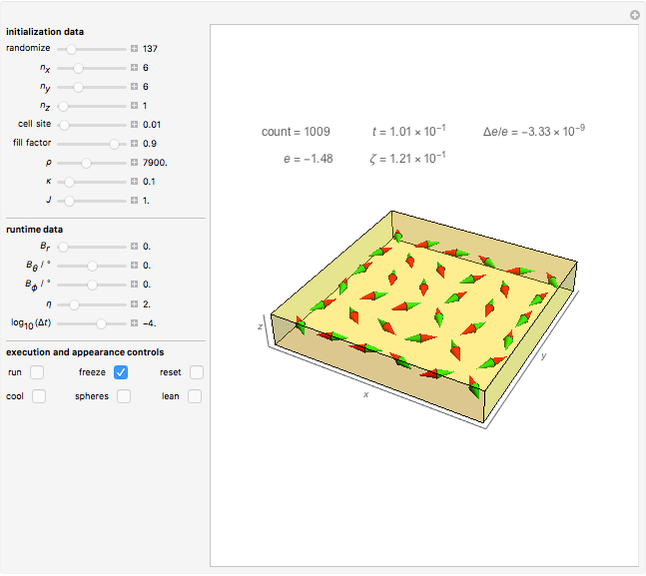
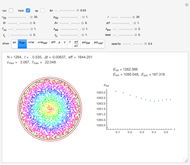
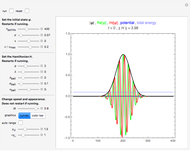
Snapshot 1: a 3D configuration resulting by decay from a well-aligned configuration
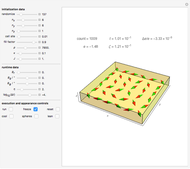
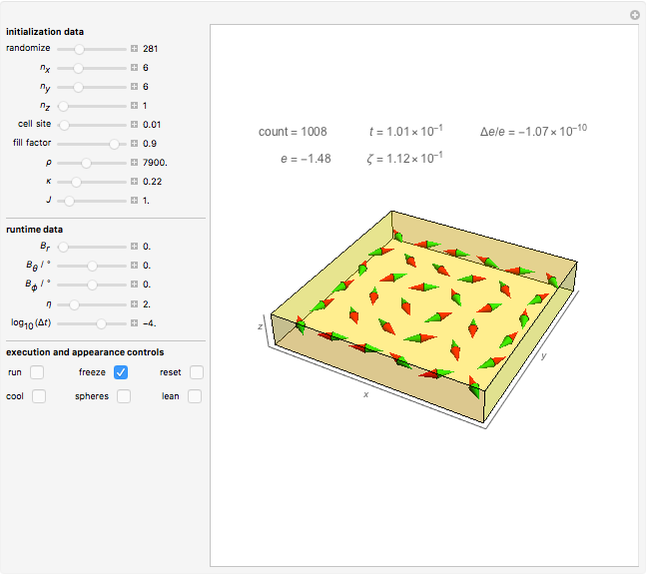
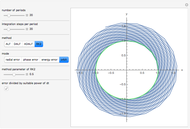
Snapshot 2: a 2D configuration resulting by decay from a well-aligned configuration
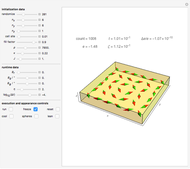
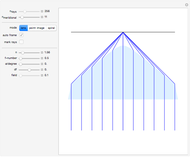
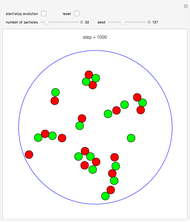
Snapshot 3: a 2D configuration resulting by decay from a not-so-well-aligned configuration
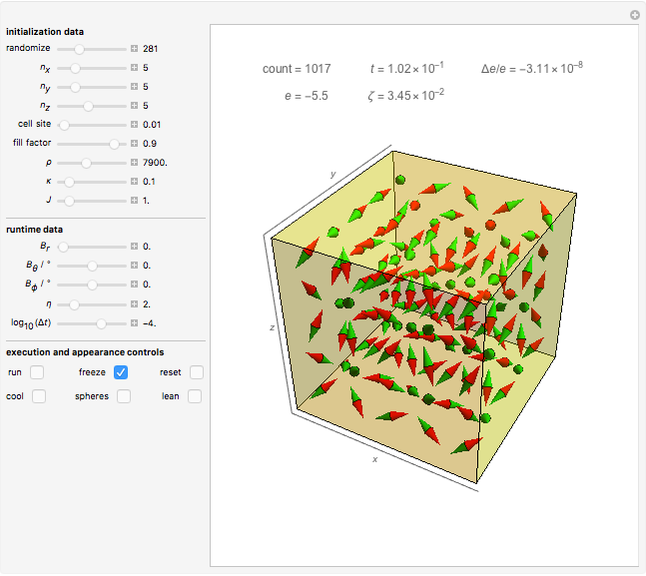
Snapshot 4: a 2D configuration resulting by decay from a random configuration
A finite part of a cubic lattice is considered where each lattice point is the center of a freely rotatable, uniformly magnetized spherical particle. Further, the particles are under the influence of a homogeneous magnetic field. The device that holds the particles in place (e.g. ball cages with diamond-coated contact surfaces) is assumed to cause negligible friction. However, friction is introduced by putting the particles into a bath of viscous liquid. This Demonstration gives numerical values (always relative to SI units without a prefix) to all these quantities and follows the time evolution of the particles in a graphic that represents the magnetic dipoles as stylized compass needles.
The dynamical algorithm for the particles makes use of Euler–Rodrigues parameters [3, 4]. 2D lattices of true compass needles were used around 1880 by the Scottish physicist J. A. Ewing for studying the patterns formed by the needles when a homogeneous magnetic field was applied and slowly varied in strength [1]. In Ewing's case, the needles work like pairs of separated magnetic poles. By contrast, uniformly magnetized spheres behave exactly like true dipoles (see [2]). Ewing's needles may have formed more stable chains than those shown in the present model.
The main lesson we learn (which was not clear to Ewing) is that well-aligned fields of magnetic dipoles always decay into ordered domains of only a few dipoles if the aligning field is switched off. Quantum mechanical exchange interaction is needed to allow for large stable, uniformly aligned magnetic domains, such as Weiss's domains in iron.
References
[1] J. A. Ewing, Magnetic Induction in Iron and other Metals, New York: The D. Van Nostrand Company, 1900. (July 2, 2018) archive.org/details/magneticinductio00ewinrich.
[2] B. F. Edwards, D. M. Riffe, J.-Y. Ji and W. A. Booth, "Interactions between Uniformly Magnetized Spheres," American Journal of Physics, 85(130), 2017. doi: 10.1119/1.4973409.
[3] U. Mutze, "Rigidly Connected Overlapping Spherical Particles: A Versatile Grain Model," Granular Matter, 8(3–4), 2006 pp. 185–194. doi:10.1007/s10035-006-0011-5.
[4] U. Mutze. "Polyspherical Grains and Their Dynamics." (July 2, 2018) www.ulrichmutze.de/articles/07-252.pdf.
Permanent Citation