Feedback Control in an Activated Sludge Reactor

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
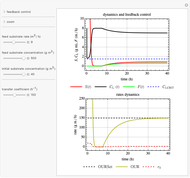
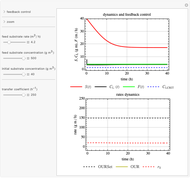
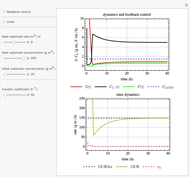
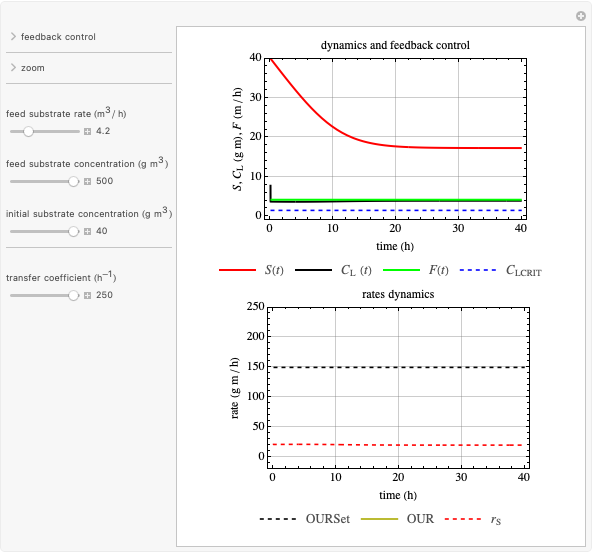
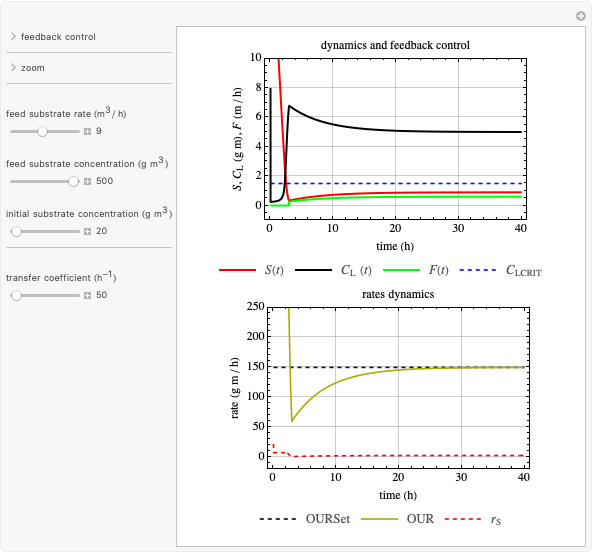
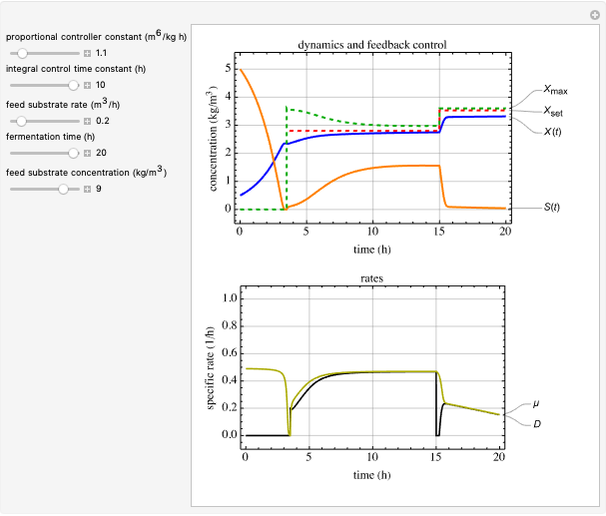
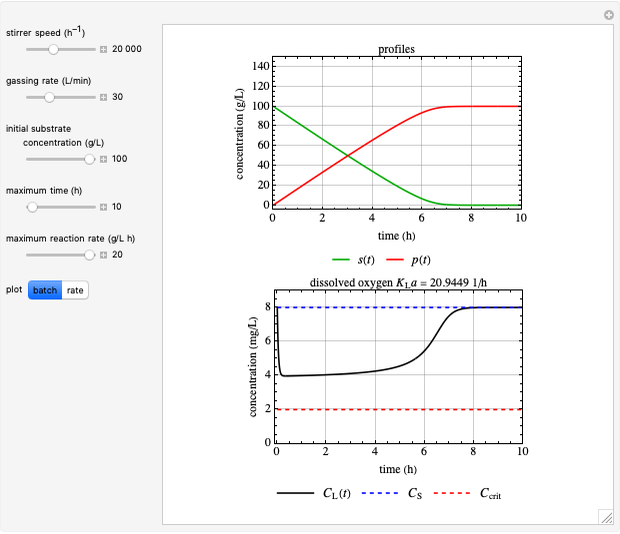
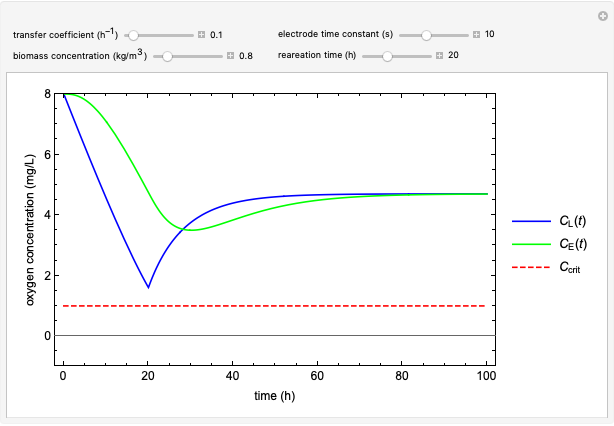
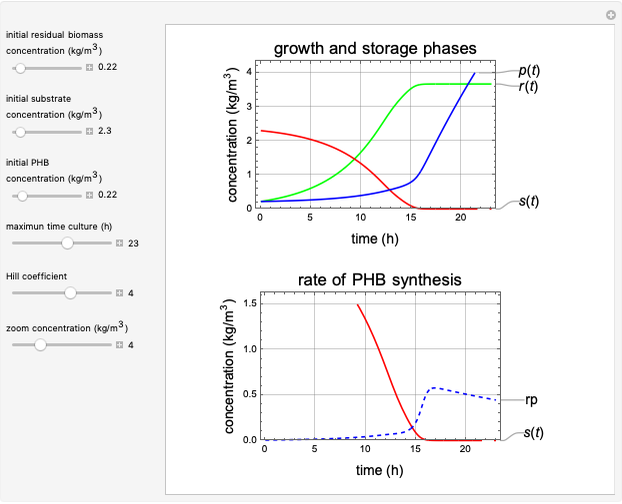
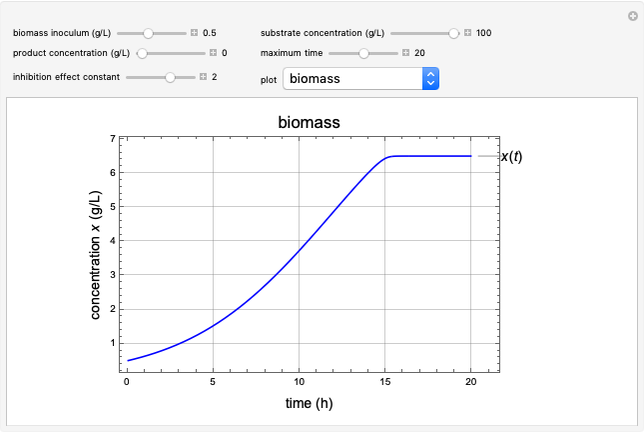
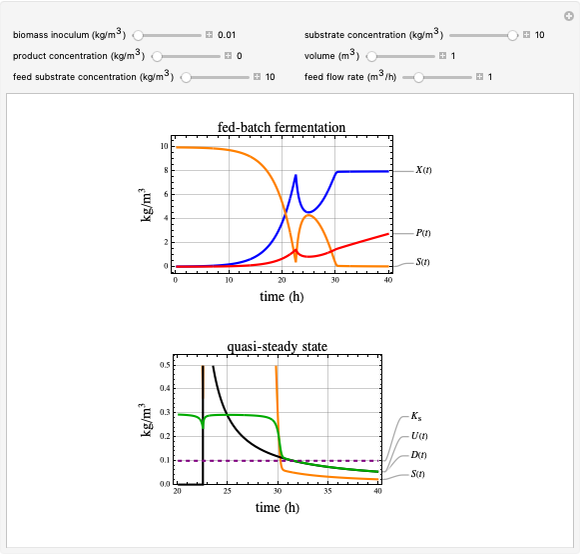
This Demonstration considers a model for the dynamics of a continuous reactor for treating an inhibitory substrate. The degradation rate is influenced by the concentrations of both the substrate and the dissolved oxygen, which are measured by an electrode. The biomass concentration is assumed constant, maintained in a sedimentation tank. Liquid phase balances for both the substrate and the dissolved oxygen are essential aspects of the model. This is important since the reactor is designed to avoid high concentrations of substrate, which would cause inhibitory behavior. This is accomplished by feeding the substrate at controlled flow rates, ensuring that the substrate concentration does not become too high.
Contributed by: R. Ricardo Sánchez (January 2023)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Notation
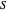 : substrate concentration
: substrate concentration 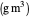
 : inhibition constant
: inhibition constant 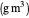
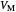 : maximum reaction velocity
: maximum reaction velocity 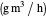
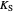 : saturation constant
: saturation constant 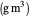
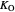 : oxygen saturation constant
: oxygen saturation constant 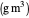
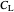 : dissolved oxygen concentration
: dissolved oxygen concentration 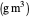
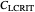 : critical dissolved oxygen concentration
: critical dissolved oxygen concentration 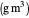
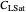 : dissolved oxygen saturation concentration or solubility of oxygen in the broth
: dissolved oxygen saturation concentration or solubility of oxygen in the broth 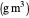
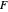 : feed substrate rate
: feed substrate rate 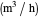
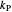 : proportional control constant
: proportional control constant 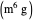
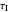 : integral control constant
: integral control constant 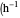 )
)
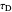 : derivative control constant
: derivative control constant 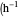 )
)
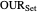 : set value for oxygen uptake rate
: set value for oxygen uptake rate 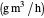
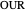 : oxygen uptake rate
: oxygen uptake rate 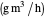
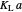 : transfer coefficient
: transfer coefficient 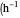 )
)
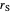 : reaction rate for substrate
: reaction rate for substrate 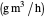
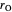 : reaction rate for oxygen
: reaction rate for oxygen 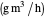
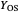 : Yield coefficient, oxygen to substrate
: Yield coefficient, oxygen to substrate
Kinetic parameters
Inhibitory substrates at high concentrations reduce the maximum reaction velocity, below that predicted by a kinetic equation. The inhibition function may be expressed empirically as:
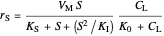 .
.
If substrate concentrations are low, the term 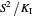 is lower in magnitude than
is lower in magnitude than 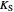 and
and 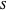 , and the inhibition function reduces to the double Monod equation. You can observe the inhibition effect on oxygen uptake rate and the dissolved oxygen concentration.
, and the inhibition function reduces to the double Monod equation. You can observe the inhibition effect on oxygen uptake rate and the dissolved oxygen concentration.
Oxygen transfer
The oxygen mass transfer rate  can be represented by:
can be represented by:
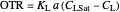 .
.
Oxygen uptake rate
The oxygen uptake rate 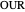 can be represented by:
can be represented by:
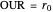 and
and 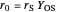 .
.
Control process
Proportional, integral and derivative control of the feed rate can be set by:

where  is the error and is represented by
is the error and is represented by 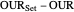 . If
. If  , then
, then  =
= 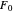 and the process runs out of control.
and the process runs out of control.
Reference
[1] J. B. Snape, I. J. Dunn, J. Ingham and J. E. Prenosil, Dynamics of Environmental Bioprocesses: Modelling and Simulation, New York: VCH, 1995.
Permanent Citation