Fugacity as a Driving Force for Mass Transfer

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
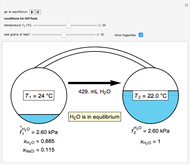
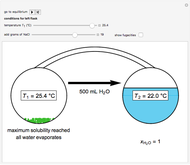
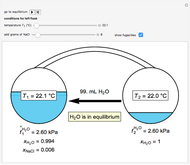
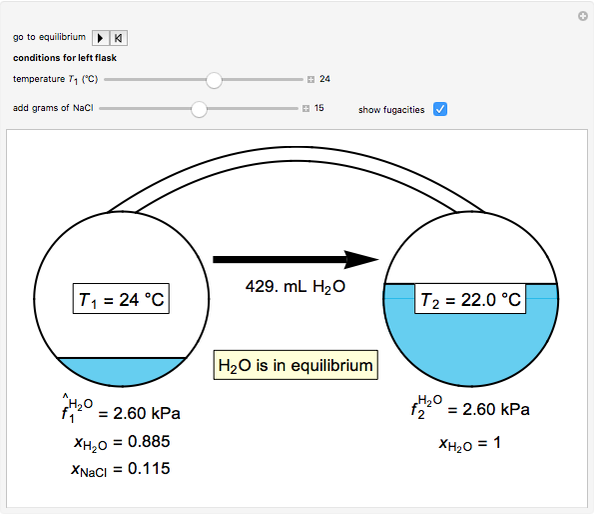
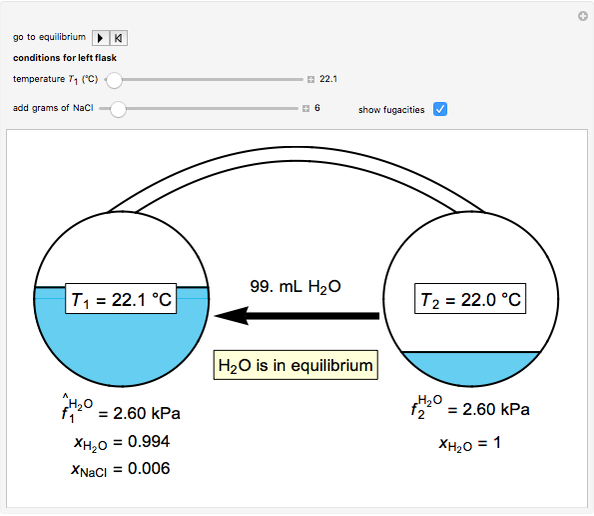
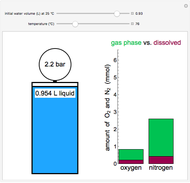
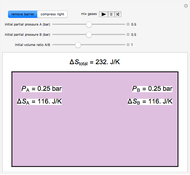
Two 1-liter flasks are at different temperatures; initially the left flask contains 500 mL of water with dissolved salt and the right flask contains 200 mL of pure water. You can control the temperature of the left flask and the amount of salt dissolved with sliders. Click the play button "go to equilibrium" to remove the caps on each flask. Water transfers from one flask to the other to try to make water fugacities equal in each flask. For some conditions, all the water transfers to the left or right flask. Check "show fugacities" to display the water fugacities in each flask.
Contributed by: Rachael L. Baumann (March 2015)
Additional contributions by: Garrison J. Vigil, John L. Falconer, and Nick Bongiardina
(University of Colorado Boulder, Department of Chemical and Biological Engineering)
Open content licensed under CC BY-NC-SA
Snapshots
Details
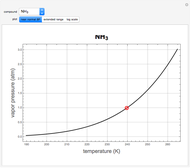
The saturation pressure of water  is calculated using the Antoine equation:
is calculated using the Antoine equation:
 ,
,
where  ,
,  and
and  are Antoine constants,
are Antoine constants,  is temperature (°C) and
is temperature (°C) and  is in units of kPa.
is in units of kPa.
The fugacity  of pure water is equal to its saturation pressure:
of pure water is equal to its saturation pressure:
 .
.
For water with dissolved salt, the fugacity of the solution  (kPa) is given by:
(kPa) is given by:
 ,
,
where  is the mole fraction of water.
is the mole fraction of water.
The screencast video at [1] explains how to use this Demonstration.
Reference
[1] Fugacity as a Driving Force for Mass Transfer [Video]. (Sep 1, 2016) www.colorado.edu/learncheme/thermodynamics/FugacityDrivingForceMassTransfer.html.
Permanent Citation