Fundamental Laws of Random Matrix Theory

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
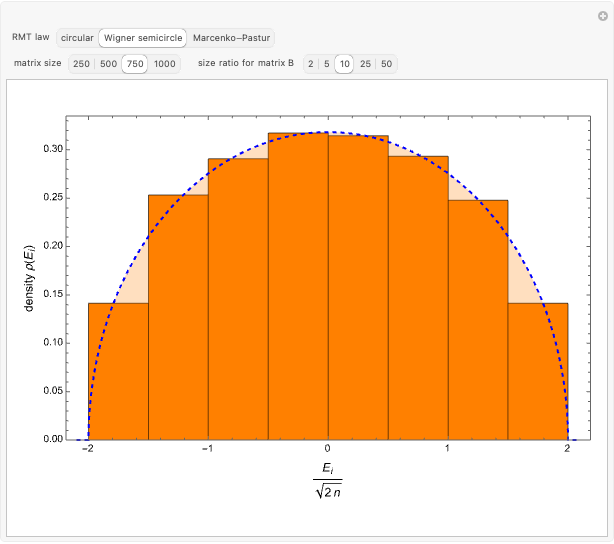
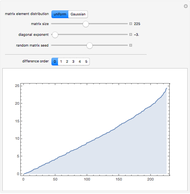
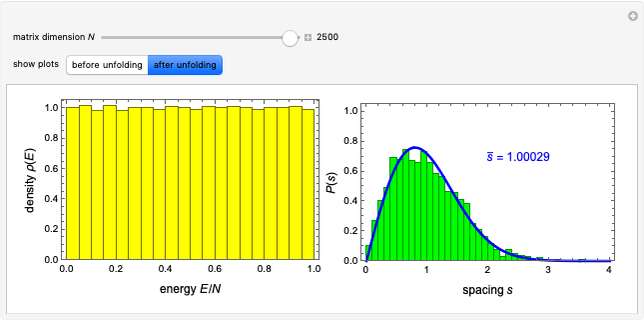
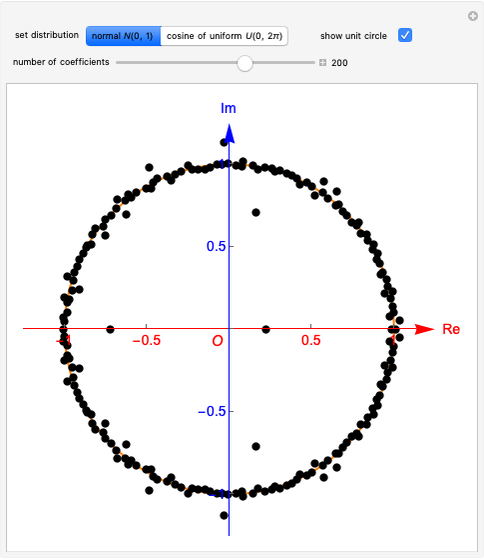
This Demonstration exhibits the three fundamental laws of random matrix theory related to the eigenvalue distributions for a selected matrix transformation. Starting from the eigenvalues of an  random matrix
random matrix  with its elements distributed according to the normal distribution with zero mean and unit variance, we can verify convergence to the circular law in the limit as
with its elements distributed according to the normal distribution with zero mean and unit variance, we can verify convergence to the circular law in the limit as  , appropriately rescaled by a factor
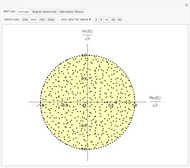
, appropriately rescaled by a factor  . Thus the limiting spectral distribution is the uniform distribution over the unit disk in the complex plane (see Related Links). You can see this by selecting the "circular" button, for
. Thus the limiting spectral distribution is the uniform distribution over the unit disk in the complex plane (see Related Links). You can see this by selecting the "circular" button, for  . You can set the matrix size by selecting the corresponding button in the second row.
. You can set the matrix size by selecting the corresponding button in the second row.
Contributed by: Jessica Alfonsi (January 2023)
(Padova, Italy)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Snapshot 1: plot corresponding to the circular law and diagonalization of a  random matrix
random matrix
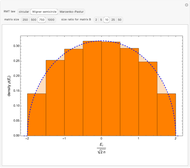
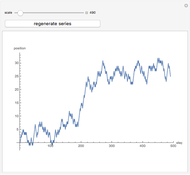
Snapshot 2: histogram density plot corresponding to Wigner semicircle law obtained by diagonalization of a  symmetrized random matrix
symmetrized random matrix
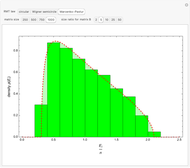
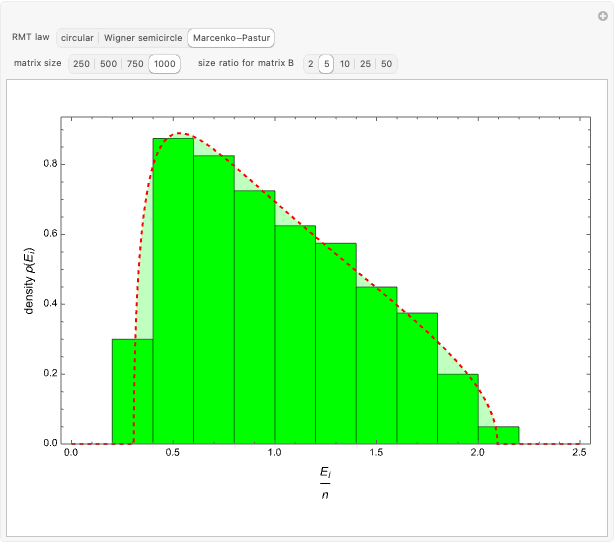
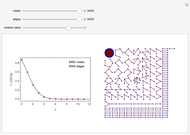
Snapshot 3: histogram density plot corresponding to Marcenko–Pastur law obtained by diagonalization of the scalar product of a  rectangular matrix
rectangular matrix
Permanent Citation