Stable Lévy Process

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
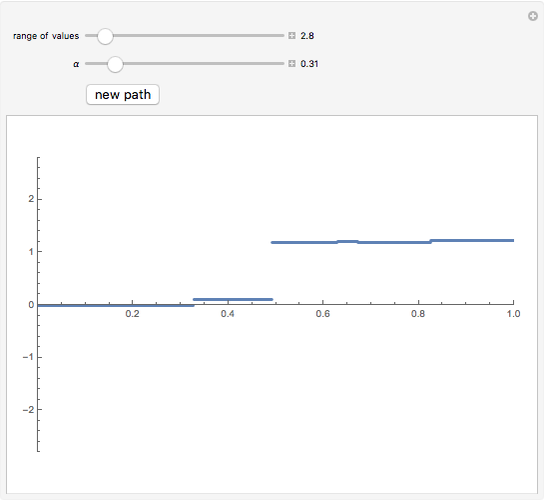
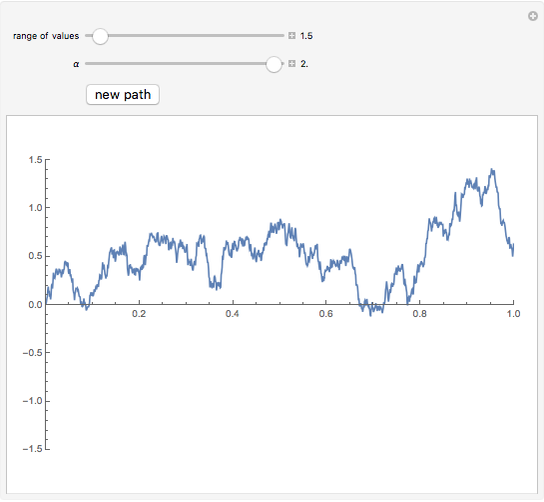
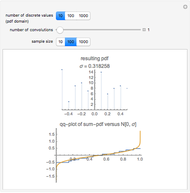
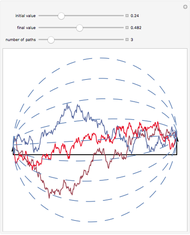
This Demonstration shows the path of a symmetric stable Lévy process. Such a process has the property of "self-similarity" with Hurst exponent  (where
(where  is the index of stability) and independent increments (unlike fractional Brownian motion, whose increments are not independent except in the case of Hurst exponent
is the index of stability) and independent increments (unlike fractional Brownian motion, whose increments are not independent except in the case of Hurst exponent  ). For
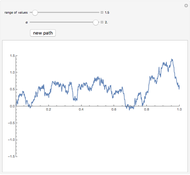
). For 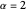 , the stable Lévy process coincides with ordinary Brownian motion. In this Demonstration, you can vary the parameter
, the stable Lévy process coincides with ordinary Brownian motion. In this Demonstration, you can vary the parameter 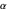 between 0 and 2 and the vertical range of the plot to zoom in and out.
between 0 and 2 and the vertical range of the plot to zoom in and out.
Contributed by: Andrzej Kozlowski (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
One of the most remarkable properties of Brownian motion  is self-similarity: for all
is self-similarity: for all  and all
and all 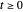 , the random variable
, the random variable  has the same distribution as
has the same distribution as  . A strictly stable Lévy process
. A strictly stable Lévy process 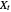 can be viewed as a generalization of Brownian motion, and has the property for all
can be viewed as a generalization of Brownian motion, and has the property for all 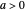 ,
,  ,
,  has the same distribution as
has the same distribution as  , for some index of stability
, for some index of stability  , where
, where 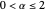 . For each index of stability
. For each index of stability  , the distributions
, the distributions  are stable distributions
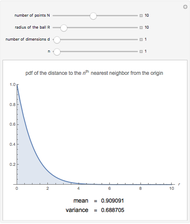
are stable distributions  . The probability density functions of this distribution are not known in explicit form except in special cases. In this Demonstration we consider the symmetric case, for which
. The probability density functions of this distribution are not known in explicit form except in special cases. In this Demonstration we consider the symmetric case, for which  . In this case the characteristic function is given by
. In this case the characteristic function is given by  , which shows that for
, which shows that for 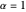 we get the Cauchy distribution and for
we get the Cauchy distribution and for  the normal distribution.
the normal distribution.
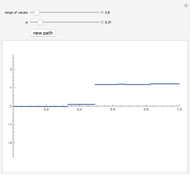
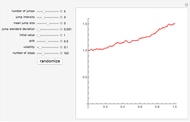
A symmetric 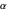 -stable process can be represented as a combination of a (compound) Poisson process and a Brownian motion. For small values of
-stable process can be represented as a combination of a (compound) Poisson process and a Brownian motion. For small values of  we see that the process is dominated by big jumps. For medium values (e.g.,
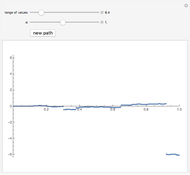
we see that the process is dominated by big jumps. For medium values (e.g.,  , i.e., Cauchy process) we get both small and large jumps. For
, i.e., Cauchy process) we get both small and large jumps. For 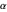 close to 2 we get Brownian motion with occasional jumps.
close to 2 we get Brownian motion with occasional jumps.
 -stable processes for
-stable processes for 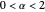 have infinite variance, which makes them somewhat inconvenient. Nevertheless, they are important in physics, biology, meteorology, and have been used in option pricing in finance.
have infinite variance, which makes them somewhat inconvenient. Nevertheless, they are important in physics, biology, meteorology, and have been used in option pricing in finance.
G. Samrodnitsky and M. Taqqu, Stable Non-Gaussian Random Processes, New York: Chapman and Hall, 1994.
A. N. Shiryaev, Essentials of Stochastic Finance, River Edge, New Jersey: World Scientific Publishing Co., 1999.
Permanent Citation