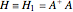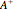Supersymmetry for the Square-Well Potential

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
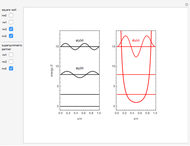
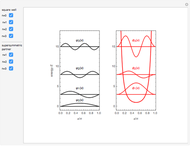
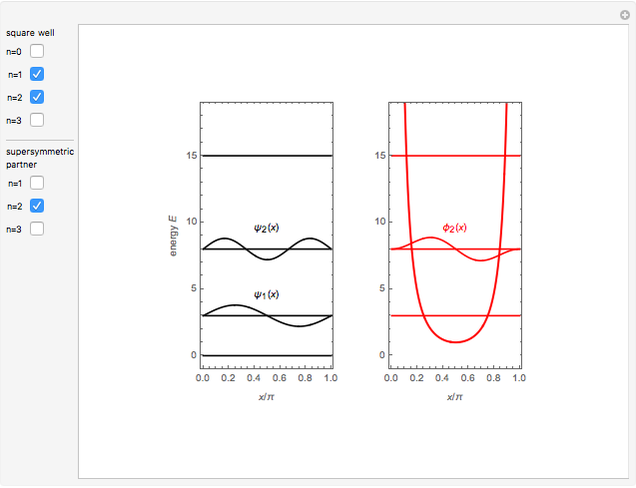
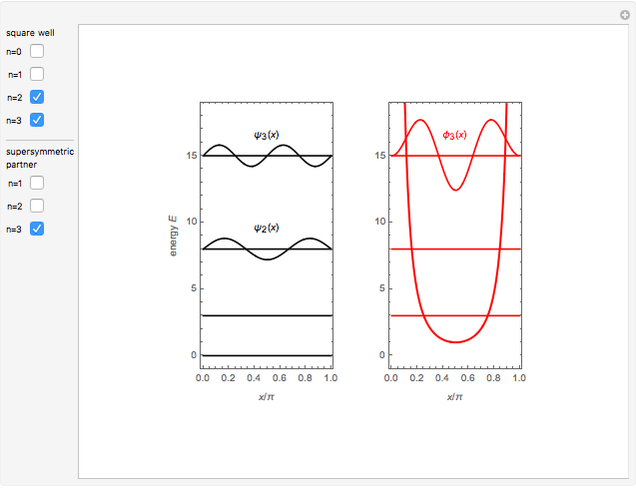
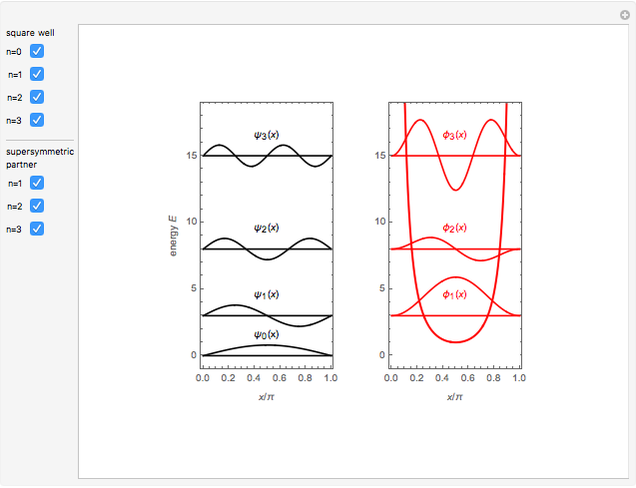
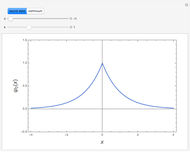
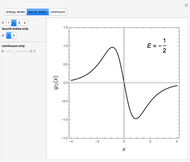
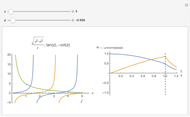
The most elementary problem in quantum mechanics considers a particle of mass  in a one-dimensional infinite square well of width
in a one-dimensional infinite square well of width  ("particle in a box"). The Schrödinger equation can conveniently be written in the modified form
("particle in a box"). The Schrödinger equation can conveniently be written in the modified form  in
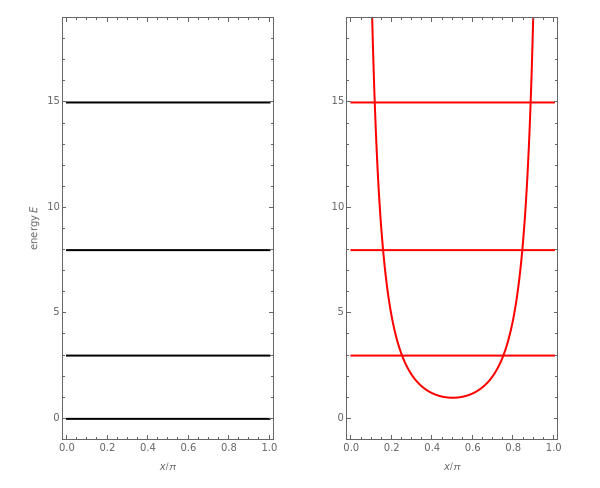
in  , such that the ground state energy is rescaled to
, such that the ground state energy is rescaled to  . The eigenstates are then given by
. The eigenstates are then given by  -1],
-1],  . The quantum number
. The quantum number  is now equal to the number of nodes in the wavefunction. For simplicity, let
is now equal to the number of nodes in the wavefunction. For simplicity, let  and
and  . The Schrödinger equation then simplifies to
. The Schrödinger equation then simplifies to  with
with  ,
,  ,
,  ,
,  .
.
Contributed by: S. M. Blinder (March 2011)
With suggestions by Jeremy Michelson
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference: A. Khare, "Supersymmetry in Quantum Mechanics," arXiv, 2004.
Permanent Citation