Illustrating the Central Limit Theorem Using the Quantile Plot for Sums of Unit Exponential Random Variables

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
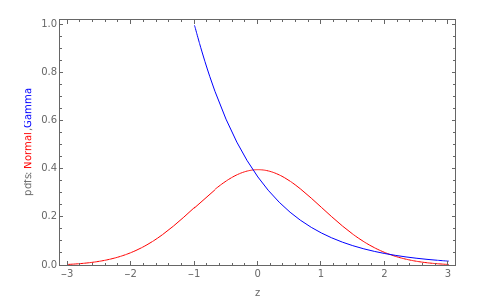
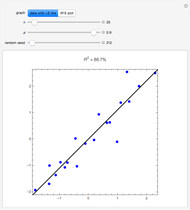
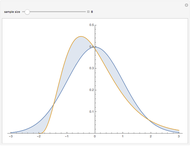
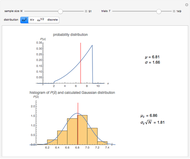
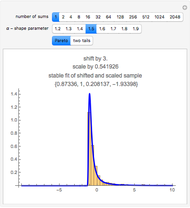
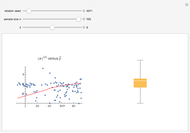
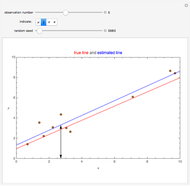
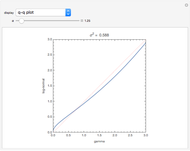
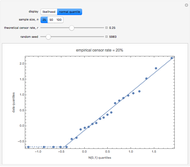
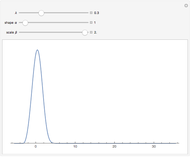
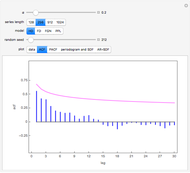
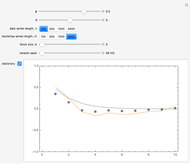
The quantile plot plots the quantiles of one distribution against the quantiles of another. It provides a visual method of comparing two distributions that is especially sensitive to departures in the tails of the distribution. In this Demonstration we construct the standardized sum of  unit exponential random variables. We compare the plot of its probability density function and the quantile plot of its quantiles versus the normal quantiles. At
unit exponential random variables. We compare the plot of its probability density function and the quantile plot of its quantiles versus the normal quantiles. At  , the pdf plot suggests the tails have converged but the quantile plot reveals that the tails of the sum are still a little bit thicker.
, the pdf plot suggests the tails have converged but the quantile plot reveals that the tails of the sum are still a little bit thicker.
Contributed by: Ian McLeod (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The quantile plot may easily be constructed using Mathematica's built-in function ParametricPlot.
The quantile plot for comparing two datasets, as in the two-sample problem, is available in Mathematica with the function QuantilePlot.
The quantile plot is also sometimes called the QQ-plot and the term quantile plot is used for a plot of  , versus
, versus  , where
, where  are the ordered data and
are the ordered data and  is the sample size [1]. Many examples of the use of both of these types of plots are given in [1].
is the sample size [1]. Many examples of the use of both of these types of plots are given in [1].
[1] W. S. Cleveland, Visualizing Data, Summit, NJ: Hobart Press, 1993.
Permanent Citation