Illustrating the Central Limit Theorem with Sums of Uniform and Exponential Random Variables
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
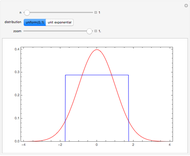
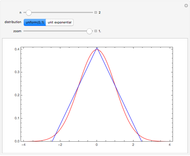
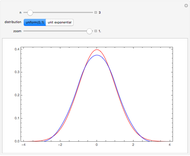
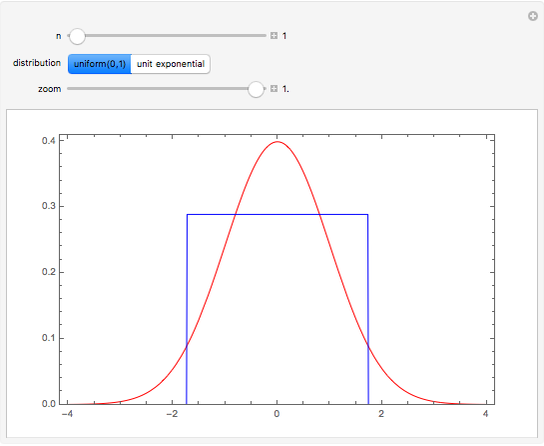
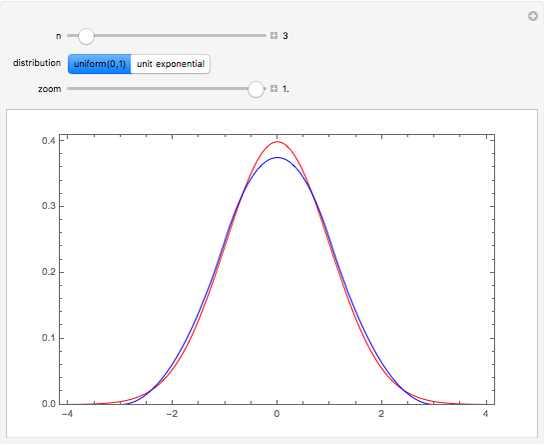
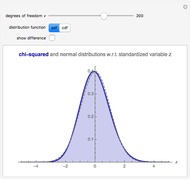
The exact probability density function (PDF) of standardized sums of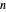 
uniform 
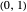or unit exponential variables is compared with the standard normal density. As 
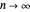, these PDFs converge to the standard normal PDF (central limit theorem).
Contributed by: Ian McLeod (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
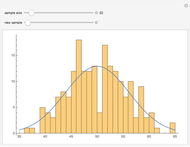
[1, p. 64] shows that the cumulative distribution function for the sum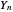 
of 
independent uniform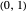 
random variables, 
, is
.
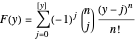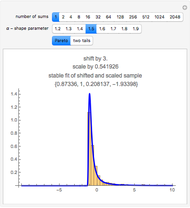
Taking the derivative, we obtain the PDF of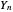 
. In the case of the unit exponential, the PDF of 
is the gamma distribution with shape parameter 
and scale parameter 
. In each case we compare the standard normal PDF with the PDF of 
, where 
and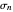 
are the mean and standard deviation of 
, respectively.
[1] N. L. Johnson and S. Kotz, Continuous Univariate Distributions, Vol. 2, Boston: Houghton Mifflin, 1970.
Permanent Citation
Sampling Distribution of the Mean and Standard Deviation in Various Populations
Ian McLeod
Mean, Median, and Quartiles in Skewed Distributions
Ian McLeod
Illustrating the Central Limit Theorem with Sums of Bernoulli Random Variables
Ian McLeod (University of Western Ontario)
Illustrating the Central Limit Theorem Using the Quantile Plot for Sums of Unit Exponential Random Variables
Ian McLeod
Central Limit Theorem for the Continuous Uniform Distribution
David K. Watson
Central Limit Theorem Illustrated with Four Probability Distributions
D. Meliga and S. Z. Lavagnino
Chi-Squared Distribution and the Central Limit Theorem
Peter Falloon
Generalized Central Limit Theorem
Roger J. Brown and Bob Rimmer
The Central Limit Theorem
Chris Boucher
Central Limit Theorem Applied to Samples of Different Sizes and Ranges
Mark D. Normand and Micha Peleg
-
Rank Transform in Harmonic Regression Time Series
Ian McLeod -
Detecting Periodicity in Short Time Series
Ian McLeod -
Tempered Fractionally Differenced White Noise
Ian McLeod -
Regression toward the Mean
Ian McLeod -
Spread-Location Regression Diagnostic Check
Ian McLeod -
Anscombe Quartet
Ian McLeod -
Visualizing Higher-Dimensional Data with 3D Scatterplots
Ian McLeod -
Mean, Fitted-Value, Error, and Residual in Simple Linear Regression
Ian McLeod -
Estimating and Diagnostic Checking in Censored Normal Random Samples
Ian McLeod -
Comparing Gamma and Log-Normal Distributions
Ian McLeod -
Monte Carlo Expectation-Maximization (EM) Algorithm
Ian McLeod -
Comparing Exact and Approximate Censored Normal Likelihoods
Ian McLeod -
Transformation to Symmetry of Gamma Random Variables
Ian McLeod -
Illustrating the Central Limit Theorem with Sums of Bernoulli Random Variables
Ian McLeod -
Hidden Correlation in Regression
Ian McLeod -
Informal Power Assessment of the Normal Probability Plot
Ian McLeod -
Time Series for Power-Law Decay
Ian McLeod -
Block Bootstrap for Time Series
Ian McLeod -
Fractional Gaussian Noise
Ian McLeod -
Plotting a Long Time Series
Ian McLeod