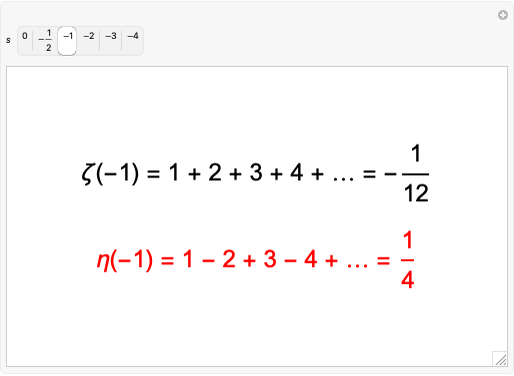
Interpretation of Some Divergent Series via the Zeta and Eta Functions
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
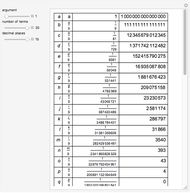
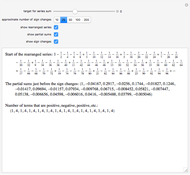
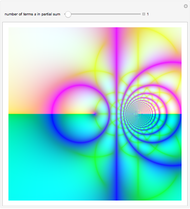
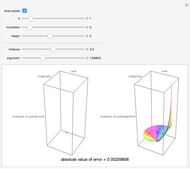
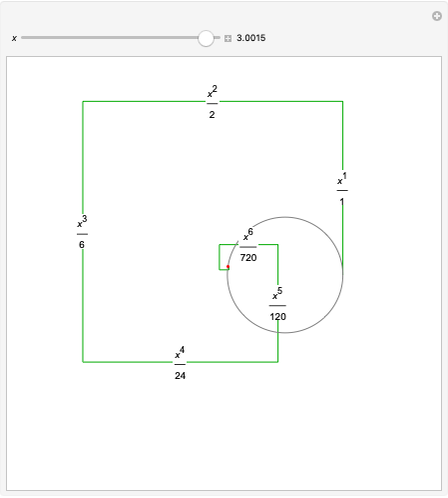
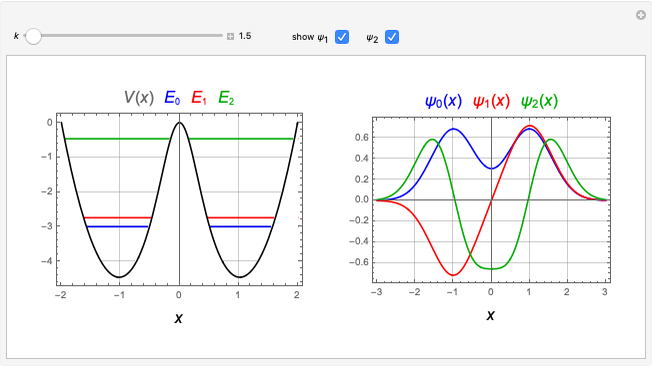
The Riemann zeta function is defined by the Dirichlet series:
[more]
Contributed by: S. M. Blinder (August 25)
Open content licensed under CC BY-NC-SA
Details
References
[1] Astounding: 1 + 2 + 3 + 4 + 5 + ... = -1/12 [Video] (May 17, 2023) youtu.be/w-I6XTVZXww.
[2] D. Overbye, "In the End, It All Adds Up to -1/12," The New York Times, Feb 3, 2014.
[3] J. G. Polchinski, String Theory: An Introduction to the Bosonic String, New York: Cambridge University Press, 2005 p. 22.
Snapshots
Permanent Citation