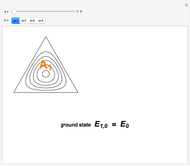
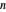Quantum Particle in a Regular Polygon by Finite Element Method
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
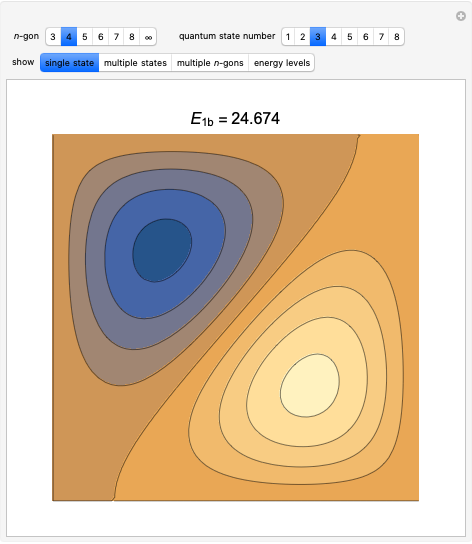
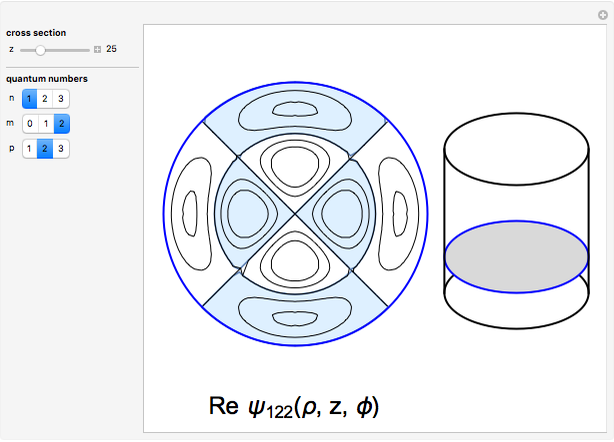
The two-dimensional Schrödinger equation for a particle confined to a regular  -gon (with
-gon (with  ) can be written (in atomic units
) can be written (in atomic units  )
)
Contributed by: S. M. Blinder (August 2022)
Open content licensed under CC BY-NC-SA
Snapshots
Details
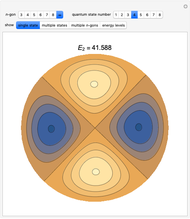
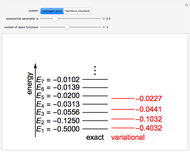
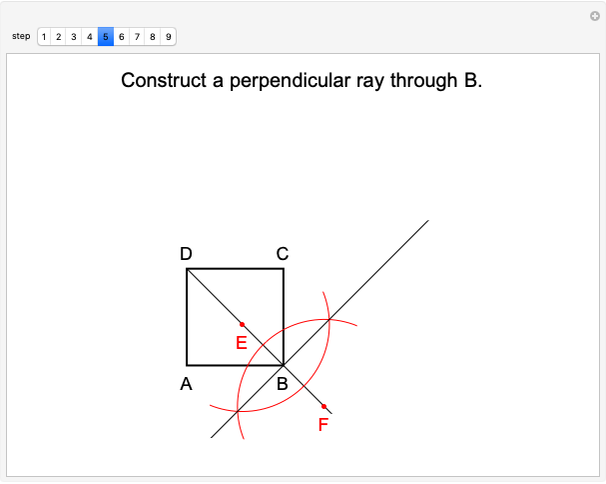
Test for particle in a square. Exact solution:
 .
.
Comparison with finite element method:
 (
( ),
),  (
( ),
),  (
( ),
),  (
( ),
),  (
( ,
,  ).
).
Reference
[1] Wikipedia. "Finite Element Method." (Jul 1, 2022). en.wikipedia.org/wiki/Finite_element_method.
Permanent Citation