Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Trilinear Coordinates in Triangle of Line Charges

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

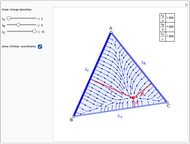
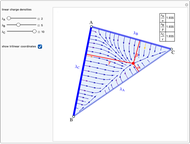
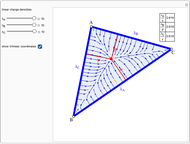
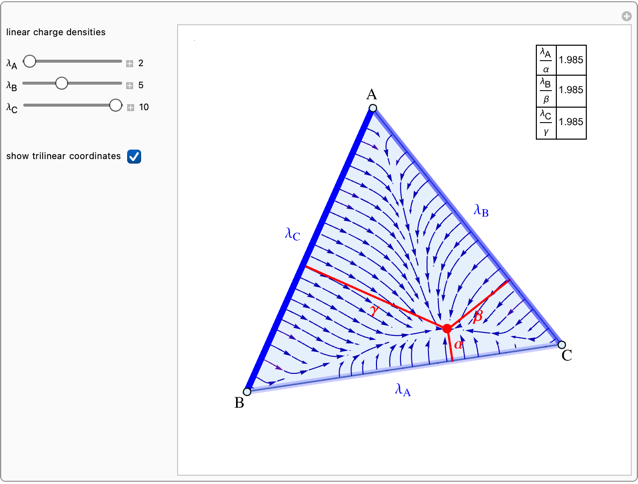
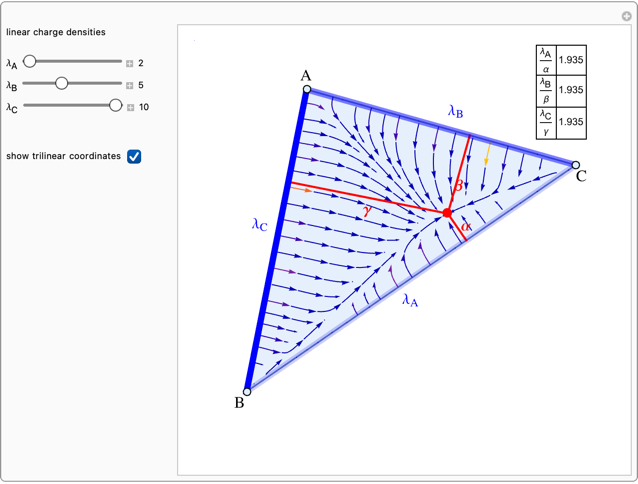
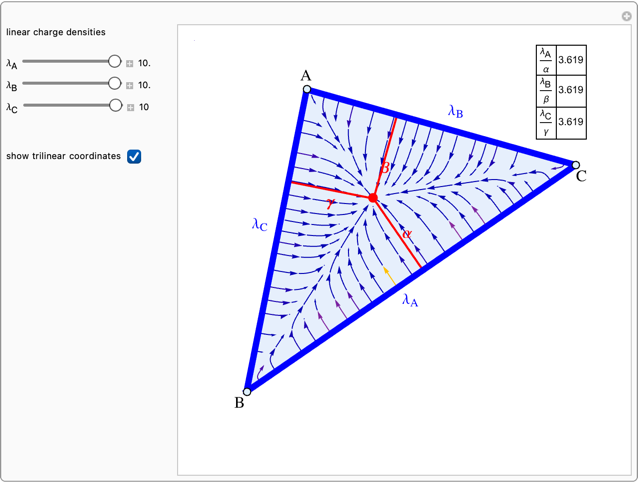
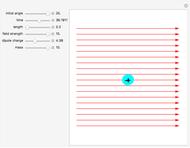
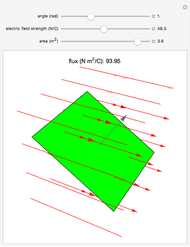
Suppose three finite line charges with positive linear charge densities , , are located on the sides opposite the vertices of the triangle . It can be shown that the electric field is zero at the point with trilinear coordinates that are in the same ratios as .

[more]

You can drag the vertices , , and vary the charge densities with the controls. The graphic shows a stream plot of the resulting electric field within the triangle.

Check "show trilinear coordinates" to see the point where the three contributions to the field cancel (where ); it has trilinear coordinates , , . The ratios of the densities to the trilinear coordinates then become equal: , as shown in the inset table.

[less]

Contributed by: S. M. Blinder (January 2023)
Open content licensed under CC BY-NC-SA

Snapshots

Details

The starting point for computation of the electric field is the potential for a finite uniformly charged rod of length and linear charge density , parallel to the axis:

.

The electric field is then given by . The total field is a superposition of three such terms, each rotated to coincide with a side of the triangle.

Reference

[1] Suren. "A New Electric Field Interpretation of Barycentric and Trilinear Coordinates." (Aug 2, 2022) https://faculty.evansville.edu/ck6/encyclopedia/ANewElectricFieldInterpretationSuren.pdf

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send