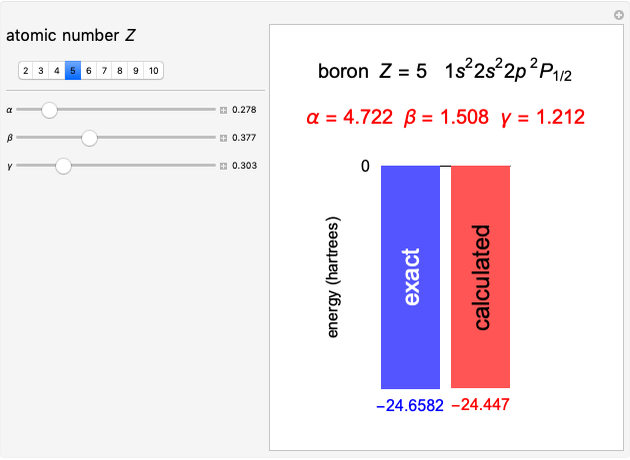
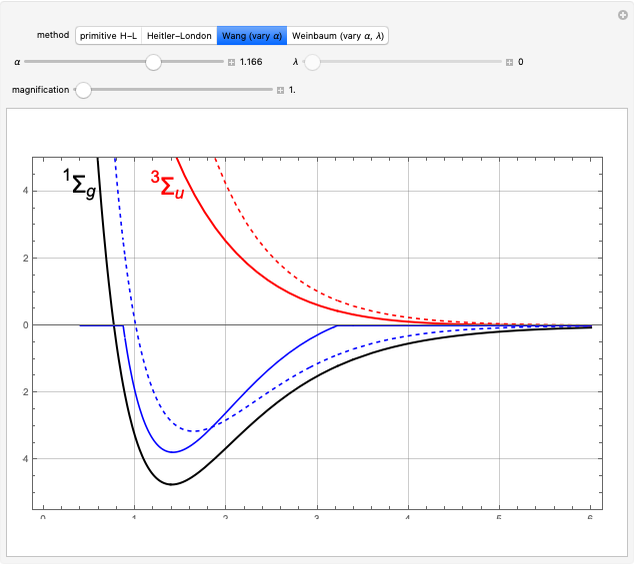
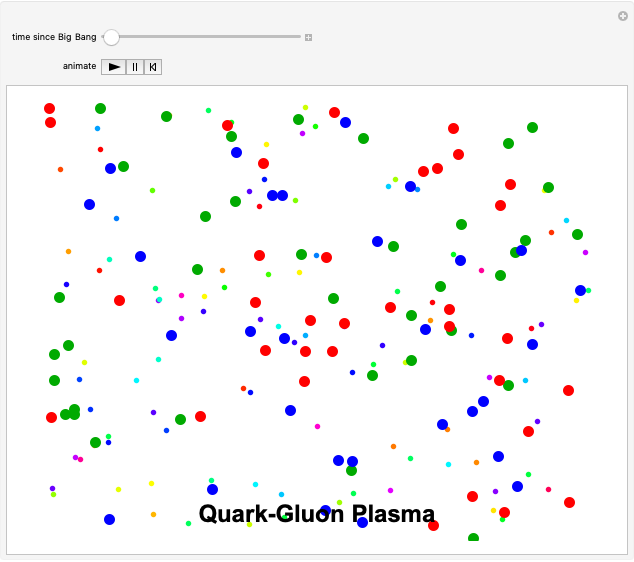
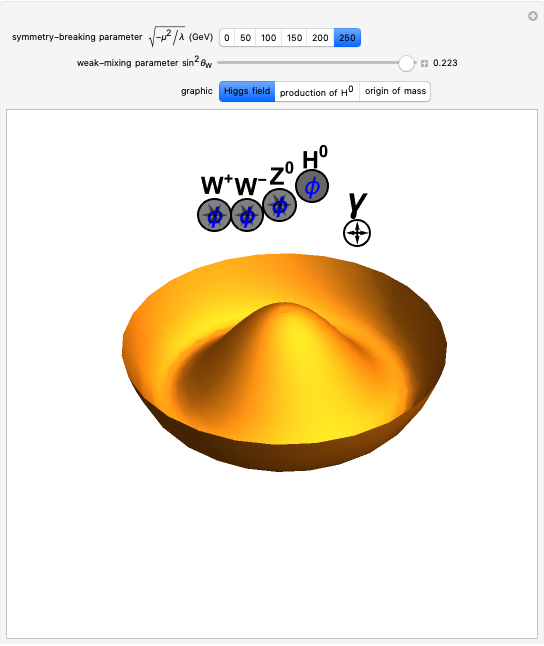
Kronig-Penney Model with Dirac Comb

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
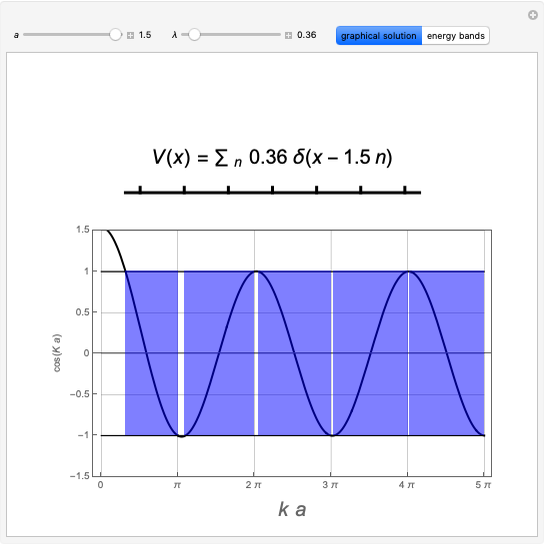
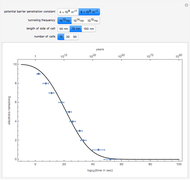
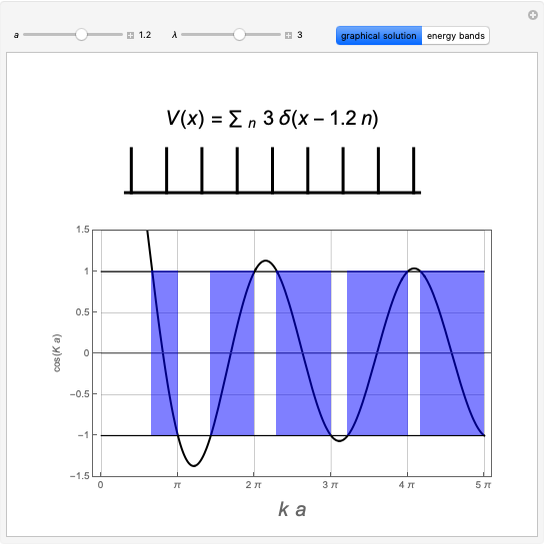
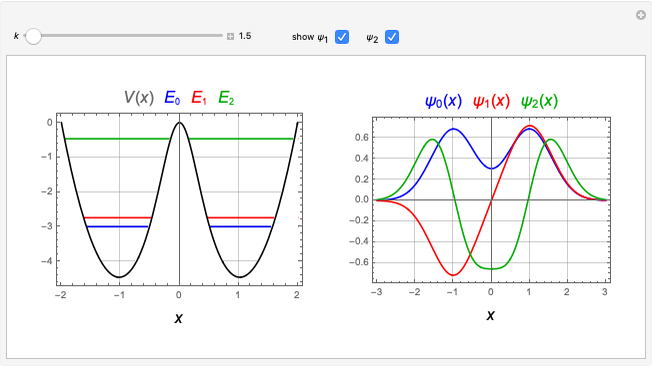
The simplest modification of the Kronig–Penney model for electrons in a one-dimensional periodic lattice can be based on a Dirac-comb potential approximating the positive cores:
[more]
Contributed by: S. M. Blinder (August 2022)
Open content licensed under CC BY-NC-SA
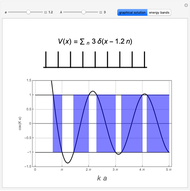
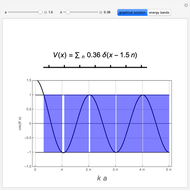
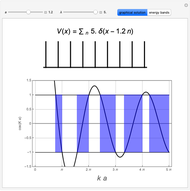
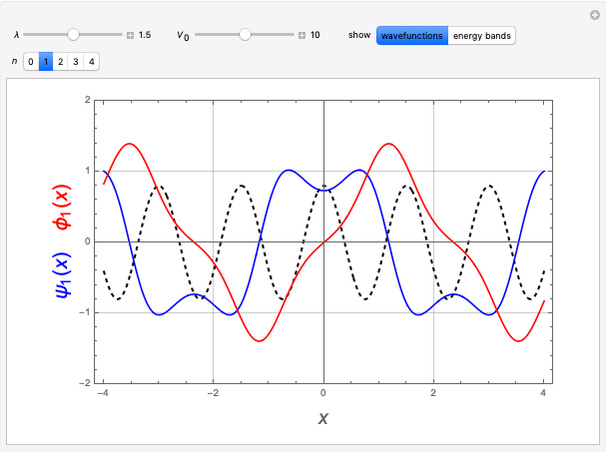
Snapshots
Details
In the interval  , the electron is a free particle and its wavefunction can be written
, the electron is a free particle and its wavefunction can be written
 .
.
For the cell immediately to the left of the origin, with  , Bloch's theorem implies that
, Bloch's theorem implies that
 .
.
The wavefunction must be continuous at  , which leads to
, which leads to
 (condition 1).
(condition 1).
The derivatives at  are found to be
are found to be
 and
and  .
.
Taking account of the discontinuity in the first derivatives, the second derivative can be written
 ,
,
which cancels the delta function in the potential when
 (condition 2).
(condition 2).
Eliminating  and
and  between the two conditions gives
between the two conditions gives
 .
.
This can be solved for  , from which it then follows that
, from which it then follows that
 .
.
References
[1] MIT OpenCourseWare. "Band Theory of Solids" (Feb 3, 2022) ocw.mit.edu/courses/chemistry/5-62-physical-chemistry-ii-spring-2008/lecture-notes/26_562ln08.pdf.
[2] S. Rajendran. "Understanding Band Structures in Solids via Solving Schrödinger Equation for Dirac Comb." (Feb 3, 2022) saravananrajendran.weebly.com/uploads/1/0/3/9/103971060/dirac_comb.pdf.
Permanent Citation