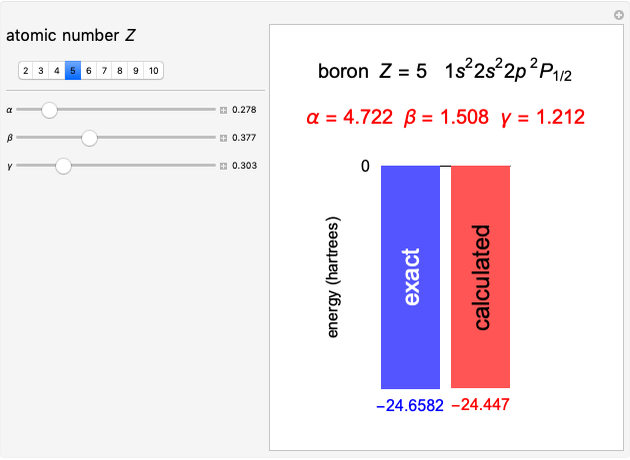
Polarizability of Hydrogen Atom

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
An electric field  distorts the charge distribution of an atom. For
distorts the charge distribution of an atom. For  states, the energy is decreased by
states, the energy is decreased by  to second order in the field strength. The parameter
to second order in the field strength. The parameter  is known as the (electric) polarizability. We consider the
is known as the (electric) polarizability. We consider the  and
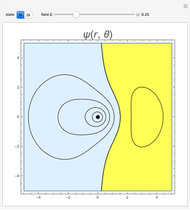
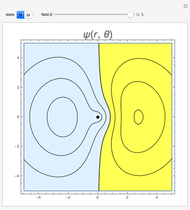
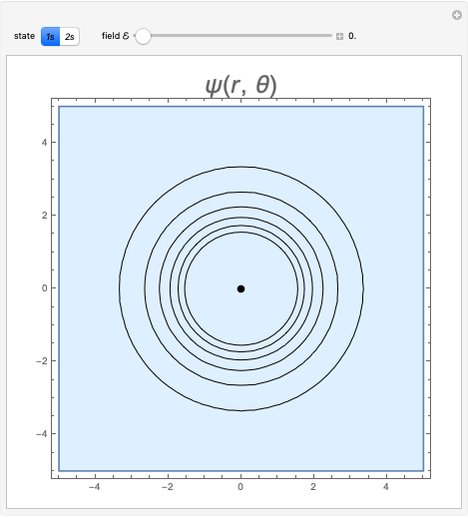
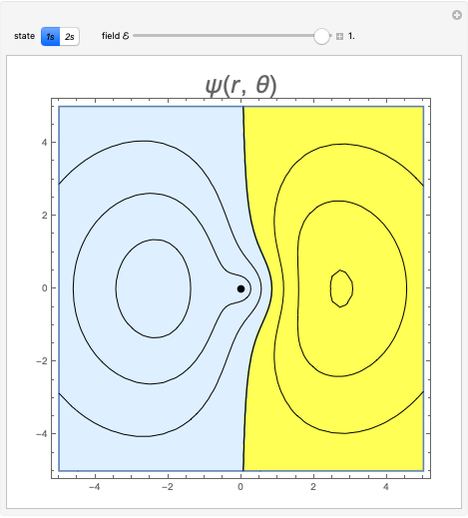
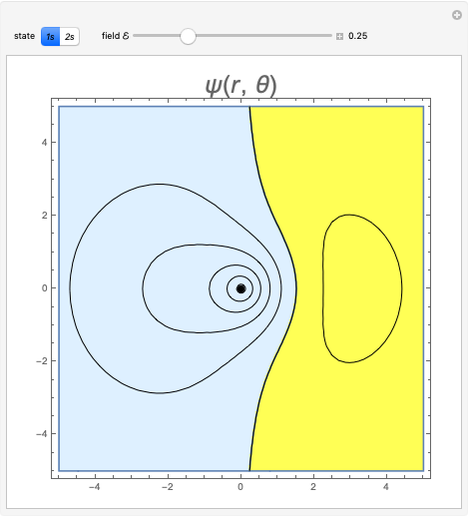
and  states of the hydrogen atom, making use of perturbation theory. The graphic shows a contour plot of the wavefunction as the electric field is increased. The wavefunction is positive in the blue region and negative in the yellow region. A similar distortion of the initially spherical charge density occurs in the formation of chemical bonds.
states of the hydrogen atom, making use of perturbation theory. The graphic shows a contour plot of the wavefunction as the electric field is increased. The wavefunction is positive in the blue region and negative in the yellow region. A similar distortion of the initially spherical charge density occurs in the formation of chemical bonds.
Contributed by: S. M. Blinder (August 2022)
Open content licensed under CC BY-NC-SA
Snapshots
Details
For the  ground state,
ground state,
 and
and  ,
,
in atomic units. The unperturbed Hamiltonian is
 ,
,
while the perturbation due to an electric field (in the  direction) is
direction) is
 .
.
The first-order perturbation equation for the  ground state is given by
ground state is given by
 (H(0)-E1(0))ψ1(1)+(H(1)-E1(1))
(H(0)-E1(0))ψ1(1)+(H(1)-E1(1)) InlineMath.
InlineMath.
The first-order energy  . We obtain thereby an inhomogeneous differential equation
. We obtain thereby an inhomogeneous differential equation
 .
.
Writing  , the differential equation reduces to
, the differential equation reduces to
 .
.
The solution that is finite for all  is
is
 .
.
Thus the ground state eigenfunction to first order is given by
 .
.
The second-order energy is obtained from
 ,
,
giving a polarizability  .
.
An analogous treatment for the  state results in the following approximation:
state results in the following approximation:
 ,
,
with a polarizability  .
.
Reference
[1] L. I. Schiff, Quantum Mechanics, 3rd ed., New York: McGraw-Hill, 1968 pp. 263–266. The approach is attributed to M. Kotani, Quantum Mechanics, Vol. I, Tokyo: Yuwanami Book Co., 1951 p. 127.
Permanent Citation