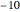Matrix Representation of the Addition Group

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
The real numbers with the operation of addition are commonly cited as an elementary example of a group. The requirements of closure, associativity, and the existence of an inverse are all fulfilled. It is well known that groups can be represented by matrices, with the group structure reflected in the corresponding matrix multiplication. So how can one reconcile representing addition by multiplication?
[more]
Contributed by: S. M. Blinder (April 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Remember the rule for multiplication of matrices:  .
.
Snapshot 1: two ways of representing 
Snapshot 2: every element (number or matrix) has an inverse
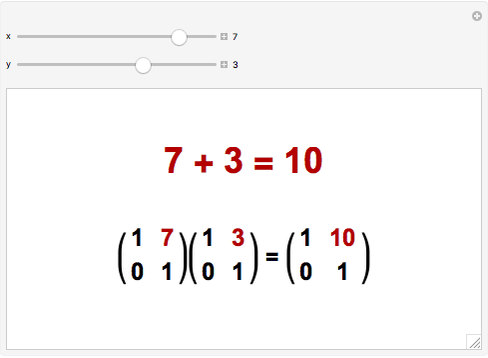
Snapshot 3: the identity element—the number 0 or the matrix 
Permanent Citation