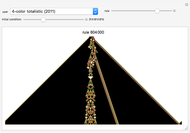
A Family of NxN Space-Filling Z-Functions, N>1

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
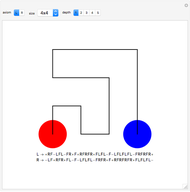
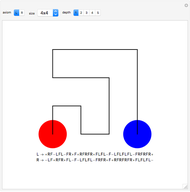
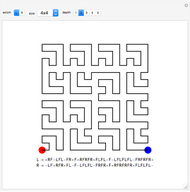
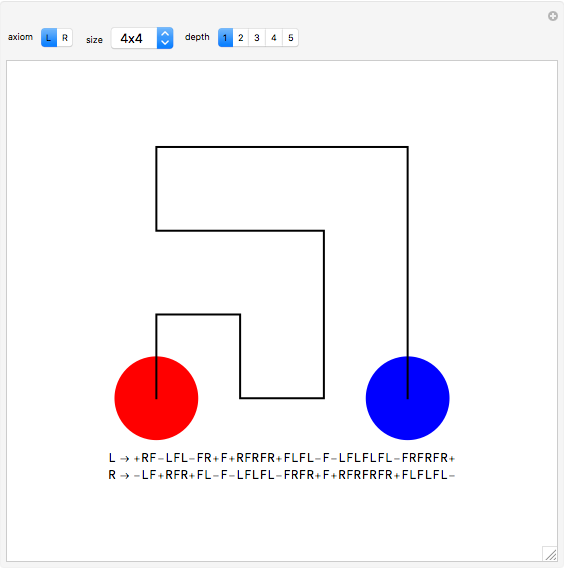
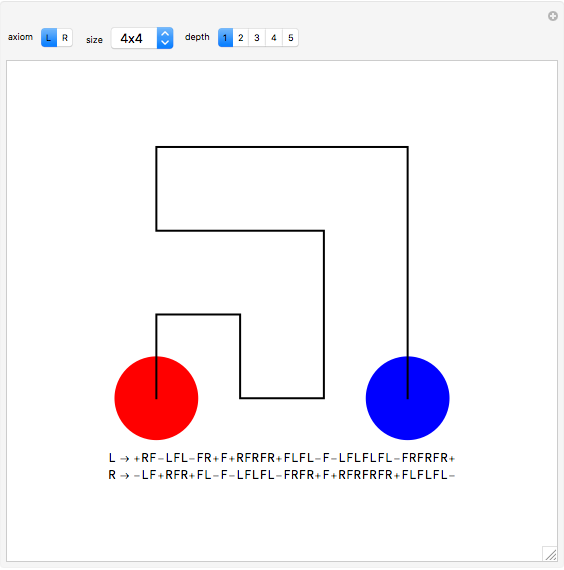
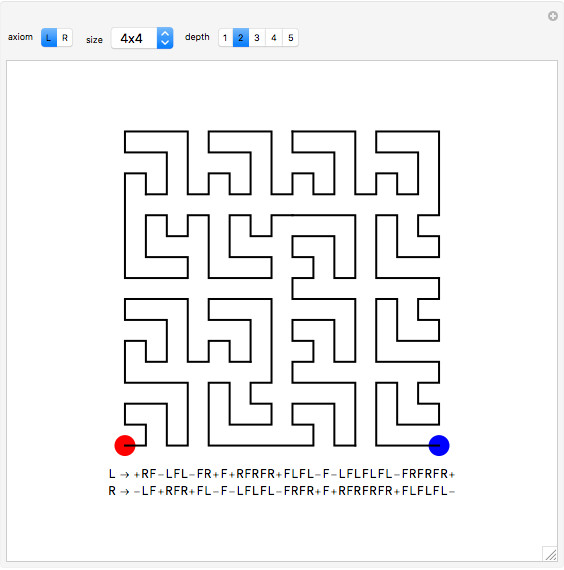
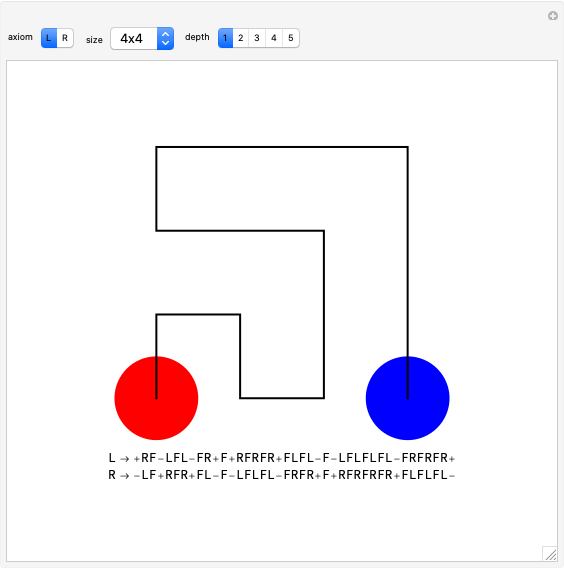
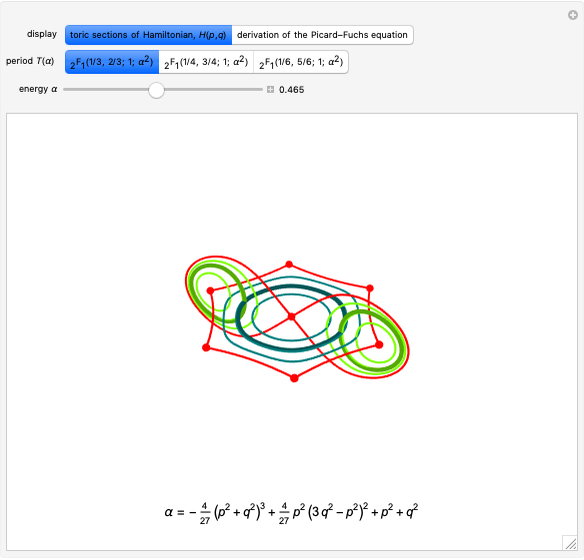
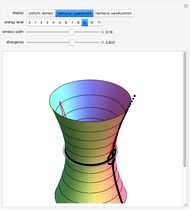
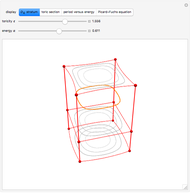
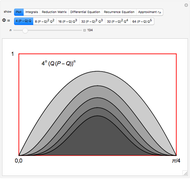
In [1], Wunderlich explores variations on Peano's space-filling curve, and in Figure 5 gives a  rule, which looks noticeably similar to Hilbert's
rule, which looks noticeably similar to Hilbert's  rule. Up to one initial "+" or "−" sign, the Lindenmayer definition of Wunderlich's Figure 5 can be obtained from the Lindenmayer definition of Hilbert's specimen, simply by concatenating additional symbols to the image words of "L" and "R" axioms. The extra symbols draw a right angle around empty squares in the complements of the
rule. Up to one initial "+" or "−" sign, the Lindenmayer definition of Wunderlich's Figure 5 can be obtained from the Lindenmayer definition of Hilbert's specimen, simply by concatenating additional symbols to the image words of "L" and "R" axioms. The extra symbols draw a right angle around empty squares in the complements of the  and
and  grids.
grids.
Contributed by: Brad Klee (October 2019)
Open content licensed under CC BY-NC-SA
Details
For an explicit implementation of the concatenation procedure, refer to the source code above.
Reference
[1] W. Wunderlich, "Über Peano-Kurven," Elemente der Mathematik, 28(1), 1973 pp. 1–10. www.mathcurve.com/fractals/wunderlich/125.pdf.
Snapshots
Permanent Citation