Weierstrass Solution of Cubic Anharmonic Oscillation

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
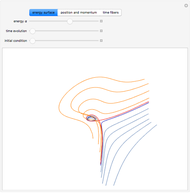
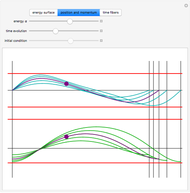
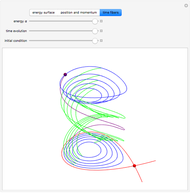
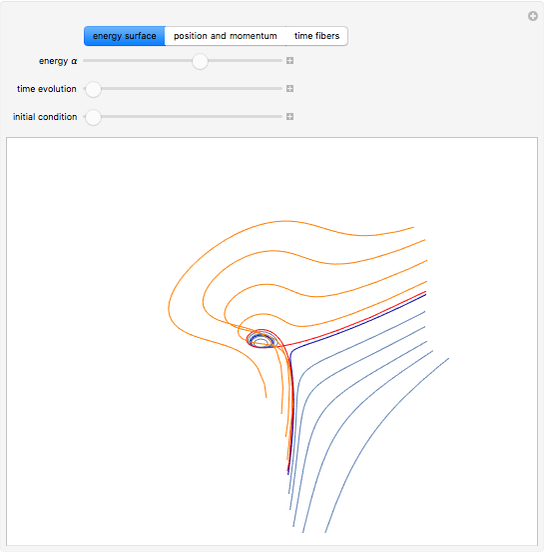
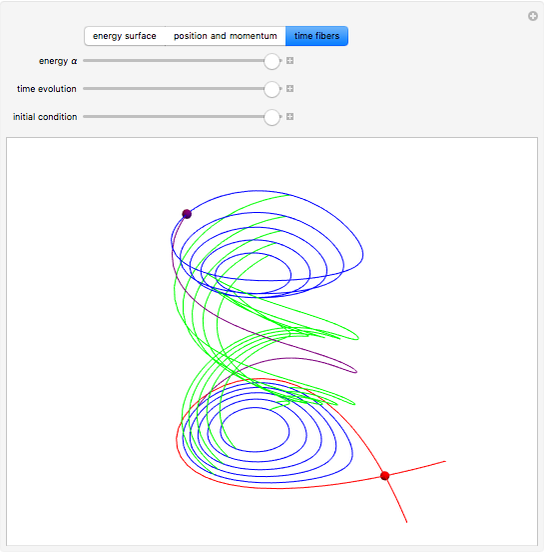
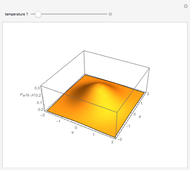
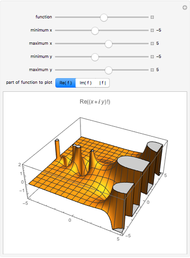
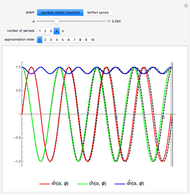
Anharmonic oscillation occurs along the Hamiltonian conserved energy surface  whenever
whenever  . Parameters
. Parameters  redefine the surface as a family of elliptic curves in the Weierstrass normal form. The Weierstrass
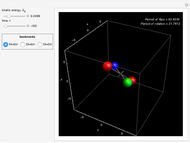
redefine the surface as a family of elliptic curves in the Weierstrass normal form. The Weierstrass  function completely determines the time parameterization and solutions to Hamilton's equations of motion [1–4]. The period of oscillation motion is given by
function completely determines the time parameterization and solutions to Hamilton's equations of motion [1–4]. The period of oscillation motion is given by  . Remarkably, this function also appears in Srinivasa Ramanujan's theory for signature-six elliptic functions [5–9].
. Remarkably, this function also appears in Srinivasa Ramanujan's theory for signature-six elliptic functions [5–9].
Contributed by: Brad Klee (February 2018)
Open content licensed under CC BY-NC-SA
Snapshots
Details
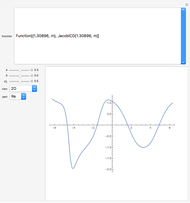
The built-in Mathematica function WeierstrassHalfPeriods does not immediately produce the identity with the Gaussian hypergeometric function. One needs to obtain this result from the integral
 ,
,
which derives from the invariant differential along the contours of the Hamiltonian energy surface. Alternative proofs may also be found in the mathematics literature [8].
This family of elliptic curves is another special case in which the Picard–Fuchs equation is simply the hypergeometric differential equation [9]. The complex period is then proportional to a second solution  .
.
References
[1] G. Pastras, "Four Lectures on Weierstrass Elliptic Function and Applications in Classical and Quantum Mechanics." arxiv.org/abs/1706.07371.
[2] A. Brizard, "Notes on the Weierstrass Elliptic Function." arxiv.org/abs/1510.07818.
[3] J. H. Silverman, The Arithmetic of Elliptic Curves, 2nd ed., New York: Springer, 2009.
[4] D. Husemöller, Elliptic Curves, 2nd ed., New York: Springer, 2004.
[5] N. J. A. Sloane and Michael Somos. The On-Line Encyclopedia of Integer Sequences. "A113424." oeis.org/A113424.
[6] B. C. Berndt, "Flowers Which We Cannot Yet See Growing in Ramanujan's Garden of Hypergeometric Series, Elliptic Functions, and q's," in Special Functions 2000: Current Perspective and Future Directions, Dordrecht: Springer, 2001 pp. 61–85. doi:10.1007/978-94-010-0818-1_ 3.
[7] S. Ramanujan, "Modular Equations and Approximations to  ," Quarterly Journal of Mathematics, 45, 1914 pp. 350–372. ramanujan.sirinudi.org/Volumes/published/ram06.pdf.
," Quarterly Journal of Mathematics, 45, 1914 pp. 350–372. ramanujan.sirinudi.org/Volumes/published/ram06.pdf.
[8] L. C. Shen, "On Three Differential Equations Associated with Chebyshev Polynomials of Degrees 3, 4 and 6," Acta Mathematica Sinica, 33(1), 2017 pp. 21–36. doi:10.1007/s10114-016-6180-1.
[9] M. Kontsevich and D. Zagier, "Periods," in Mathematics Unlimited—2001 and Beyond (B. Engquist and W. Schmid, eds.), Berlin, Heidelberg: Springer, 2001 pp. 771–808. www.maths.ed.ac.uk/~aar/papers/kontzagi.pdf.
Permanent Citation