D4 Symmetric Stratum of Quartic Plane Curves

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
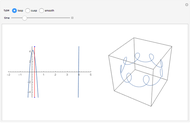
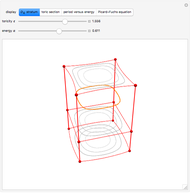
The quartic Hamiltonian form  determines a stratum of plane curves with
determines a stratum of plane curves with  symmetry. The toricity
symmetry. The toricity  distinguishes between layers of the stratum. Each planar layer contains a family of Hamiltonian level curves, indexed by energy
distinguishes between layers of the stratum. Each planar layer contains a family of Hamiltonian level curves, indexed by energy  . Allowing the coordinate variables to take on complex values associates each plane curve to a Riemann surface
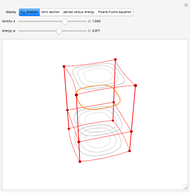
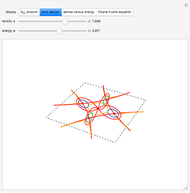
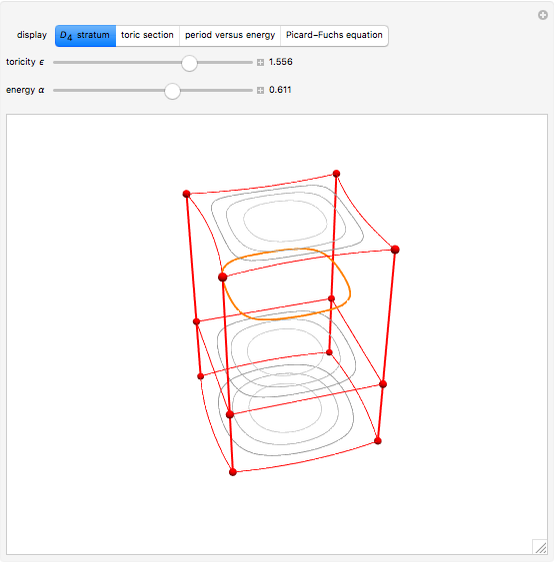
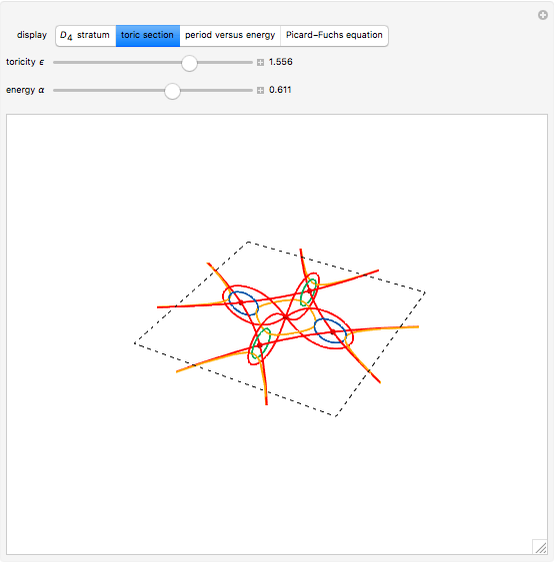
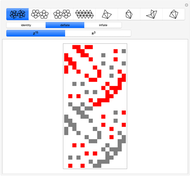
. Allowing the coordinate variables to take on complex values associates each plane curve to a Riemann surface  with nontrivial topology. This Demonstration depicts a toric section of
with nontrivial topology. This Demonstration depicts a toric section of  and gives a functional form
and gives a functional form  for period integrals taken around orthogonal contours (see Details).
for period integrals taken around orthogonal contours (see Details).
Contributed by: Brad Klee (September 2018)
Open content licensed under CC BY-NC-SA
Details
In this analysis, coordinate variables  take on complex values from
take on complex values from  (or
(or  ). The Hamiltonian function
). The Hamiltonian function  has four lines of reflection symmetry in a plane spanned by the real coordinates
has four lines of reflection symmetry in a plane spanned by the real coordinates  and
and  . Each line
. Each line  and
and  intersects one circular point and two hyperbolic points. Reflection symmetry allows us to construct real-valued contours,
intersects one circular point and two hyperbolic points. Reflection symmetry allows us to construct real-valued contours,

of the Riemann surface,
 .
.
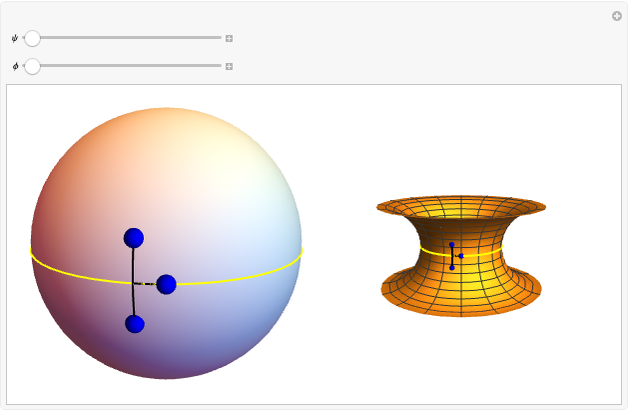
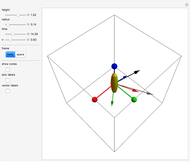
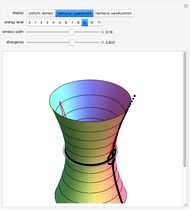
The surface  is a two-dimensional subset of a four-dimensional space and thus resists geometric intuition. Nevertheless, we color the
is a two-dimensional subset of a four-dimensional space and thus resists geometric intuition. Nevertheless, we color the  cross sections and arrange them along
cross sections and arrange them along  to suggest the underlying topology. The depiction of this Demonstration raises
to suggest the underlying topology. The depiction of this Demonstration raises  to
to  above
above  and
and  to
to  above
above  . Curve
. Curve  meets each curve
meets each curve  and
and  in four real points of intersection. The transformation model preserves dihedral symmetry up to a permutation of colors (dimensions).
in four real points of intersection. The transformation model preserves dihedral symmetry up to a permutation of colors (dimensions).
To get a general idea of time dynamics along  , we calculate period integrals along the contour curves. Transforming to action-angle variables,
, we calculate period integrals along the contour curves. Transforming to action-angle variables,
 ,
,
reduces the Hamiltonian from quartic to quadratic degree,
 .
.
Solving  for the root
for the root  leads directly to the period-energy function,
leads directly to the period-energy function,
 ,
,
with the loop integral taken around the curve  . Regardless of toricity, the period function
. Regardless of toricity, the period function  obviously converges on a region
obviously converges on a region  . Adapting an algorithm from [1], we routinely produce a Picard–Fuchs type differential equation. Application of the left operator,
. Adapting an algorithm from [1], we routinely produce a Picard–Fuchs type differential equation. Application of the left operator,
 ,
,
to integrand  makes for a sum over derivatives,
makes for a sum over derivatives,
 .
.
Such a sum necessarily leaves a remainder on the right-hand side,  . The certificate function
. The certificate function
 ,
,
contributes to an exact differential  , which integrates to zero on a complete cycle around
, which integrates to zero on a complete cycle around  , that is,
, that is,  . The Picard–Fuchs differential equation
. The Picard–Fuchs differential equation  follows immediately.
follows immediately.
Definition of the complex period function  around either curve
around either curve  or
or  follows from a beautiful symmetry. Inversion of parameters,
follows from a beautiful symmetry. Inversion of parameters,
 ,
,
acts on annihilation operator  as a scale transformation,
as a scale transformation,
 .
.
However, annihilation relations are scale free, so the transformation property implies an identity between real and complex periods,
 ,
,
with real period defined as  . Both functions
. Both functions  and
and  have the same series expansion coefficients, quickly generated by a
have the same series expansion coefficients, quickly generated by a  -recurrence (the Frobenius solution of the Picard–Fuchs equation with two initial values). Our plot of these functions uses a dynamic sum over 500 powers of
-recurrence (the Frobenius solution of the Picard–Fuchs equation with two initial values). Our plot of these functions uses a dynamic sum over 500 powers of  to achieve adequate convergence.
to achieve adequate convergence.
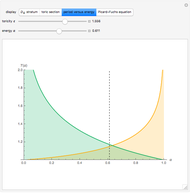
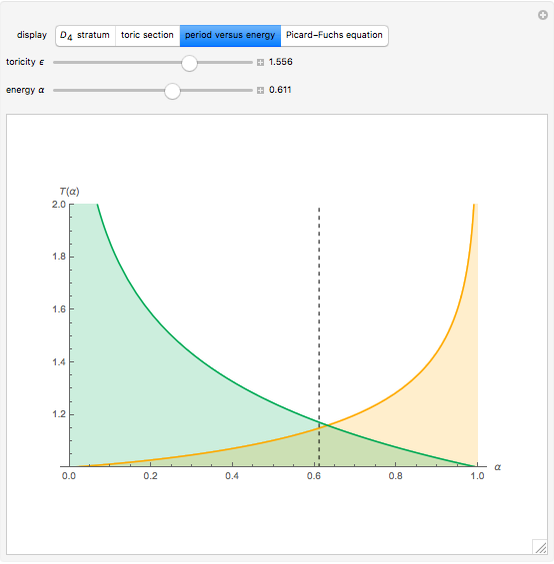
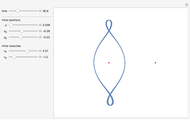
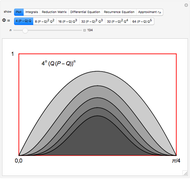
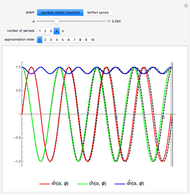
The graph of period functions  and
and  obviously shows energy inversion symmetry at the elliptic fixed point
obviously shows energy inversion symmetry at the elliptic fixed point  . This special configuration corresponds to Edwards's family of elliptic curves [2], with genus
. This special configuration corresponds to Edwards's family of elliptic curves [2], with genus  and period function
and period function
 .
.
The differential equation  takes a hypergeometric form. In straightforward analysis of
takes a hypergeometric form. In straightforward analysis of  and
and  , we find that boundary values
, we find that boundary values  also allow solutions in terms of Gauss's hypergeometric function
also allow solutions in terms of Gauss's hypergeometric function  (see [3–5]). However, the stratum limits do not lead to families of elliptic curves. For nonsingular curves
(see [3–5]). However, the stratum limits do not lead to families of elliptic curves. For nonsingular curves  , toricity parameter
, toricity parameter  determines the genus,
determines the genus,
 .
.
To prove the validity of function  , observe the self-intersection topology of curve
, observe the self-intersection topology of curve  in the limit
in the limit  (see [6]).
(see [6]).
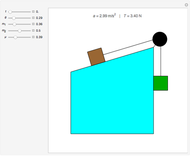
The fixed point  is also an expectation value. We give a dataset for the librational motion of a plane pendulum over a wide range of energies [7]. The data allows construction of a likelihood function with variation of the toricity
is also an expectation value. We give a dataset for the librational motion of a plane pendulum over a wide range of energies [7]. The data allows construction of a likelihood function with variation of the toricity  . It is then possible to fit function
. It is then possible to fit function  to period versus energy data at
to period versus energy data at  precision.
precision.
References
[1] B. Klee, "Approximating Pi with Trigonometric-Polynomial Integrals" from the Wolfram Demonstrations Project—A Wolfram Web Resource. demonstrations.wolfram.com/ApproximatingPiWithTrigonometricPolynomialIntegrals.
[2] H. Edwards, "A Normal Form for Elliptic Curves," Bulletin of the American Mathematical Society, 44, 2007 pp. 393–422. doi:10.1090/S0273-0979-07-01153-6. ams.org
[3] N. J. A. Sloane. "The On-Line Encyclopedia of Integer Sequences." (Sep 14, 2018) oeis.org/A002894.
[4] N. J. A. Sloane. "The On-Line Encyclopedia of Integer Sequences." (Sep 14, 2018) oeis.org/A113424.
[5] N. J. A. Sloane. "The On-Line Encyclopedia of Integer Sequences." (Sep 14, 2018) oeis.org/A318417.
[6] S. S. Abhyankar and C. L. Bajaj, "Computations with Algebraic Curves", Symbolic and Algebraic Computation: ISSAC 1988 (P. Gianni, ed.), Berlin, Heidelberg: Springer, 1989. doi:10.1007/3-540-51084-2_26.
[7] B. Klee, "Fidget Spinner Libration Data," (Sep 25, 2018) wolframcloud.com.
Snapshots
Permanent Citation