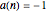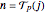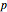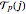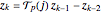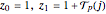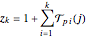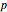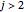Factoring the Even Trigonometric Polynomials of A269254

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
From reference [2] comes a question regarding the linear recurrence of A269254[1], 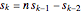 with
with 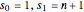 ; let
; let 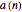 be the smallest index
be the smallest index  such that
such that 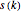 is prime, or
is prime, or  if no such
if no such  exists. For what
exists. For what  does the sequence visit
does the sequence visit 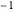 ?
?
Contributed by: Brad Klee (December 2017)
Open content licensed under CC BY-NC-SA
Details
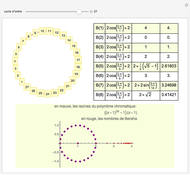
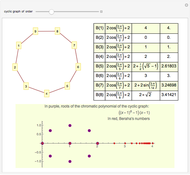
Here, the Chebyshev polynomials  are defined in an unusual way [3]:
are defined in an unusual way [3]:
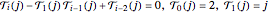 .
.
With these conventions, the first few  are
are
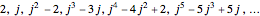
and
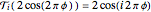 ,
,
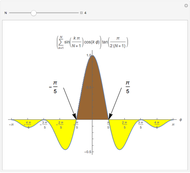
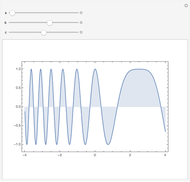
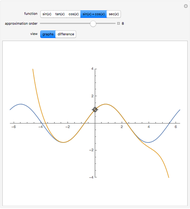
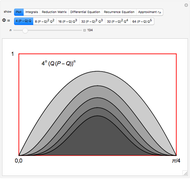
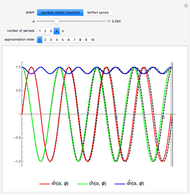
which provides a means to plot all 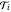 summations as wavefunctions over the domain
summations as wavefunctions over the domain 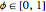 , as shown in the plots.
, as shown in the plots.
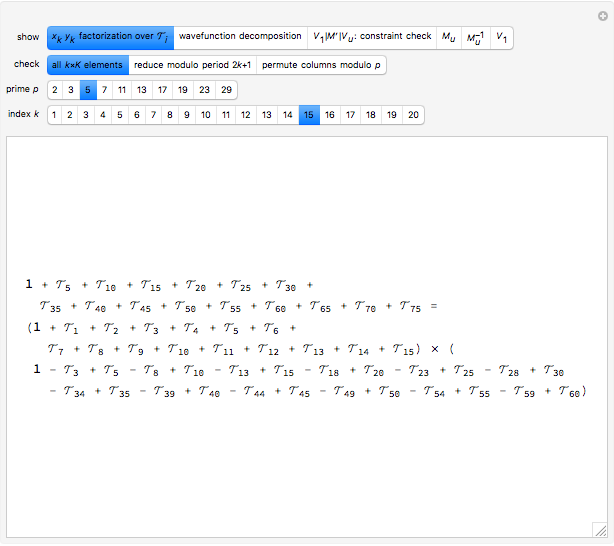
For odd primes, the factorization 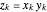 requires piecewise decomposition. We always have
requires piecewise decomposition. We always have
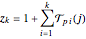 .
.
In the exceptional cases where 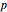 divides
divides 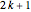 ,
,
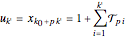 ,
,
 ,
,
with 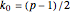 . Otherwise, if
. Otherwise, if 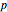 does not divide
does not divide  ,
,
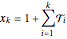 ,
,
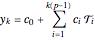 .
.
This definition leaves  coefficients undetermined. To find the
coefficients undetermined. To find the 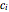 , next we substitute the ansatz into
, next we substitute the ansatz into  ,
,
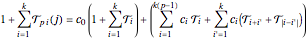 ,
,
which requires the product-sum identity,
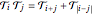 .
.
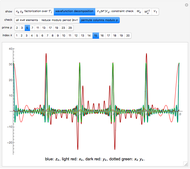
On the left- and right-hand sides, we gather constant terms and the coefficients of every  . This makes for
. This makes for 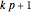 total constraints. The system of equations is overdetermined relative to
total constraints. The system of equations is overdetermined relative to 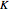 unknowns
unknowns 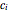 . Reading as
. Reading as 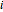 decreases from
decreases from 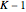 , coefficient
, coefficient 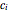 first appears as a multiplier of
first appears as a multiplier of 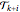 . It is then trivial to solve all
. It is then trivial to solve all 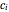 in succession where
in succession where 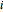 decreases. Yet the solution may not be consistent with all constraints. Define
decreases. Yet the solution may not be consistent with all constraints. Define  lower constraints from the constant term and from coefficients of
lower constraints from the constant term and from coefficients of 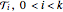 and
and 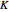 upper constraints from the coefficients of
upper constraints from the coefficients of 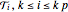 . The factorization
. The factorization 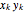 exists if and only if the solution of the
exists if and only if the solution of the  upper constraints also satisfies the
upper constraints also satisfies the  lower constraints, that is, if the over-determined system of equations is consistent. In practice, we solve the system of equations using matrices and vectors.
lower constraints, that is, if the over-determined system of equations is consistent. In practice, we solve the system of equations using matrices and vectors.
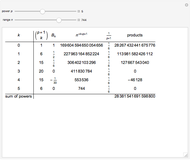
With matrices and vectors defined above in code, and with vector 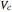 containing the
containing the 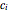 as elements, the upper and lower constraints are written as
as elements, the upper and lower constraints are written as
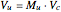 ,
,
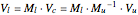 ;
;
however, when 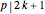 , the system of equations is inconsistent. In these exceptional cases,
, the system of equations is inconsistent. In these exceptional cases,
 .
.
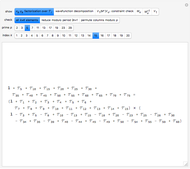
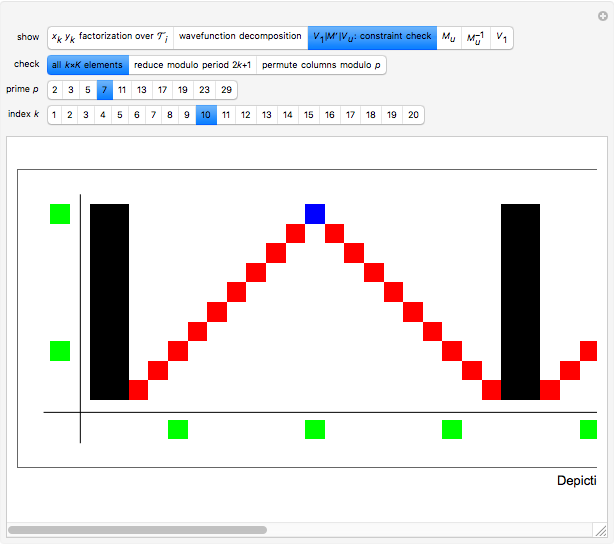
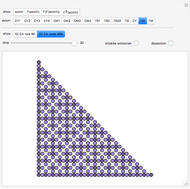
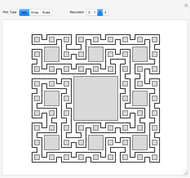
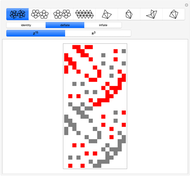
To explain the case splitting, the Demonstration shows as array plots the 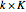 dimensional matrix
dimensional matrix 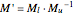 , the right of the
, the right of the  -dimensional periodic vector
-dimensional periodic vector 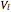 and the
and the 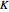 -dimensional periodic vector
-dimensional periodic vector 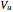 . The color rules are:
. The color rules are:

If  , then
, then 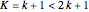 and the extra constraints
and the extra constraints 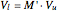 are always satisfied. If
are always satisfied. If  , then
, then 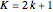 and the constraint check fails only when
and the constraint check fails only when 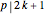 . For all higher cases,
. For all higher cases, 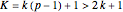 , and the constraint check again fails only when
, and the constraint check again fails only when  . In nonexceptional cases, to evaluate the dot product by rows, we first reduce modulo
. In nonexceptional cases, to evaluate the dot product by rows, we first reduce modulo  and then permute the columns by the prime period,
and then permute the columns by the prime period,  . This technique vastly improves on earlier case-by-case analysis [3, 5, 6].
. This technique vastly improves on earlier case-by-case analysis [3, 5, 6].
Solvability of the system of equations is proven by pattern analysis of the matrices here defined and depicted as array plots. Detailed analysis could be the subject for a longer journal-style explication including rigorous proofs of all factorizations presented here.
References
[1] N. J. A. Sloane, The On-Line Encyclopedia of Integer Sequences. "Define a Sequence by 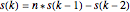 , with
, with  ; then
; then  Is the Smallest Index
Is the Smallest Index  Such That
Such That  Is Prime, or
Is Prime, or 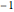 if No Such
if No Such  Exists." oeis.org/A269254.
Exists." oeis.org/A269254.
[2] H. Havermann, "A269254" (thread). SeqFan. (Oct 21, 2017) list.seqfan.eu/pipermail/seqfan/2017-October/018013.html.
[3] B. Klee, "Proof for A269254" (thread). SeqFan. (Oct 22, 2017) list.seqfan.eu/pipermail/seqfan/2017-October/018016.html.
[4] A. Hone, "A269254, A034807 and Chebyshev Polynomials" (thread). SeqFan. (Oct 27, 2017) list.seqfan.eu/pipermail/seqfan/2017-October/018052.html.
[5] B. Klee, "Re: A269254, A034807 and Chebyshev Polynomials" (thread). SeqFan. (Oct 29, 2017) list.seqfan.eu/pipermail/seqfan/2017-October/018063.html.
[6] B. Klee, "Proof Algorithm for Composite Cases of A269254" from Wolfram Community—A Wolfram Web Resource. (Dec 13, 2017) community.wolfram.com/groups/-/m/t/1209741.
[7] A. Hone, "On a Family of Sequences Related to Chebyshev Polynomials", arXiv:1802.01793[math.nt], 2018. arxiv.org.
Snapshots
Permanent Citation