Isoperiodic Potentials via Series Expansion

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
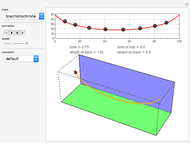
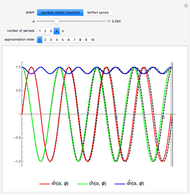
In a one-dimensional oscillation obeying conservation of energy, the potential function determines the period of motion  as a function of dimensionless energy
as a function of dimensionless energy  . However, the period function
. However, the period function  only uniquely determines the potential
only uniquely determines the potential  in the case of parity symmetry, where
in the case of parity symmetry, where  . In all other cases, it is possible to construct an uncountable infinity of potentials with the same period
. In all other cases, it is possible to construct an uncountable infinity of potentials with the same period  . Regardless of symmetry, we call any two potentials isoperiodic if they have the same period function
. Regardless of symmetry, we call any two potentials isoperiodic if they have the same period function  [1]. Careful examination of inverse functions leads to a precise definition of isoperiodic potentials using power series expansion [2]. As in [3], we use a phase-space technique to write
[1]. Careful examination of inverse functions leads to a precise definition of isoperiodic potentials using power series expansion [2]. As in [3], we use a phase-space technique to write  as a function of the potential expansion coefficients around a stable minima. The general form of
as a function of the potential expansion coefficients around a stable minima. The general form of  leads to a set of linear constraints between the expansion coefficients of isoperiodic potentials (see Details).
leads to a set of linear constraints between the expansion coefficients of isoperiodic potentials (see Details).
Contributed by: Brad Klee (April 2017)
Open content licensed under CC BY-NC-SA
Snapshots
Details
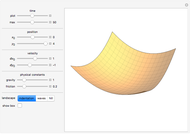
For details of published calculations, see [1, 2]. Our approach follows [3]. Starting with a Hamiltonian
 ,
,
we transform to the polar coordinates of phase space
 ,
,
where  . The preceding algorithm approximately solves this implicit equation by series inversion, producing a truncated sum
. The preceding algorithm approximately solves this implicit equation by series inversion, producing a truncated sum
 .
.
The corresponding approximate period is then calculated using
 .
.
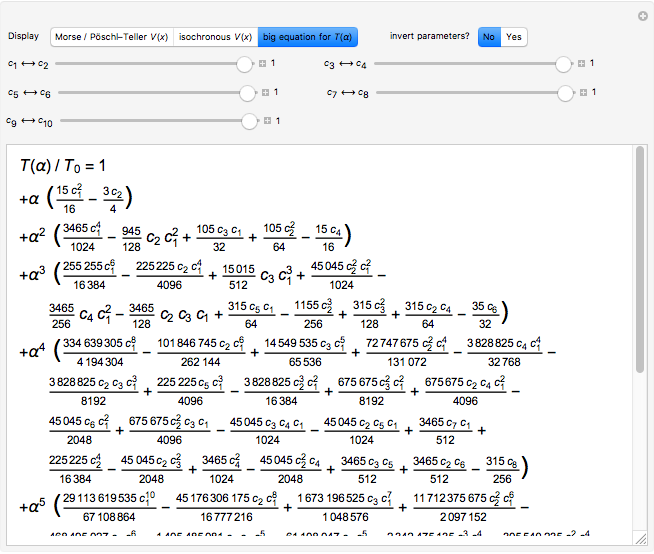
Analyzing the general period function  first reported in [4], we prove that every power of the Hamiltonian energy
first reported in [4], we prove that every power of the Hamiltonian energy  attaches to a function of the potential expansion coefficients
attaches to a function of the potential expansion coefficients  with a pair
with a pair  that does not occur in the coefficient of any
that does not occur in the coefficient of any  with
with  . This fact allows order-by-order construction of isoperiodic potentials as series expansions around a stable minima.
. This fact allows order-by-order construction of isoperiodic potentials as series expansions around a stable minima.
The isoperiodic constraint between two distinct potentials with expansion coefficients  and
and  is
is
 .
.
Fixing the  values and applying the isoperiodic constraint to the
values and applying the isoperiodic constraint to the  yet leaves one continuous degree of freedom in every coefficient
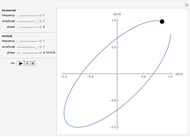
yet leaves one continuous degree of freedom in every coefficient  . These continuous degrees of freedom are controlled by sliders in this Demonstration, which directly enables you to calculate a range of isoperiodic potentials. Methods used here have also contributed to award-winning posts on Wolfram Community [5, 6].
. These continuous degrees of freedom are controlled by sliders in this Demonstration, which directly enables you to calculate a range of isoperiodic potentials. Methods used here have also contributed to award-winning posts on Wolfram Community [5, 6].
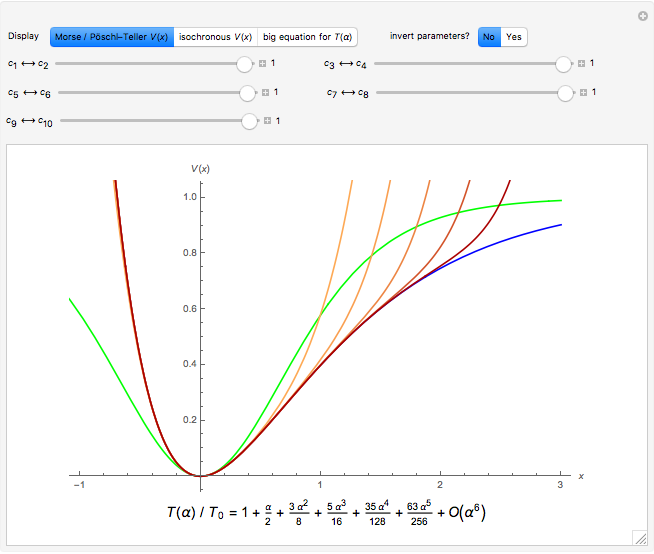
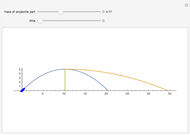
By direct evaluation of the period function for the expansion coefficients of the Morse potential and the Pöschl–Teller potential, it is possible to prove approximate isoperiodicity order-by-order, as in the commented code at the end of the initialization section. Comparing coefficients, we expect direct evaluation of both period integrals to yield
 .
.
References
[1] M. Asorey, J. F. Cariñena, G. Marmo and A. Perelomov, "Isoperiodic Classical Systems and Their Quantum Counterparts," Annals of Physics, 322(6), 2007 pp. 1444–1465. doi:10.1016/j.aop.2006.07.003.
[2] E. T. Osypowski and M. G. Olsson, "Isynchronous Motion in Classical Mechanics," American Journal of Physics, 55(8), 1987 pp. 720–725. doi:10.1119/1.15063.
[3] B. Klee, "Plane Pendulum and Beyond by Phase Space Geometry." arxiv.org/abs/1605.09102.
[4] The On-Line Encyclopedia of Integer Sequences. (Apr 4, 2017) oeis.org/A276816.
[5] B. Klee, "A Period Function for Anharmonic Oscillations" from Wolfram Community—A Wolfram Web Resource. (Apr 4, 2017) community.wolfram.com/groups/-/m/t/984488.
[6] B. Klee, "Plotting the Contours of Deformed Hyperspheres" from Wolfram Community—A Wolfram Web Resource. (Apr 4, 2017) community.wolfram.com/groups/-/m/t/1023763.
Permanent Citation