Orienting a Spin with a Magnetic Field

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
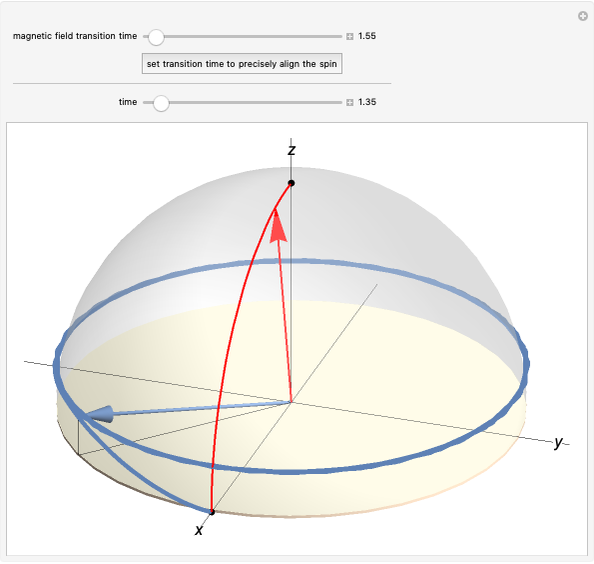
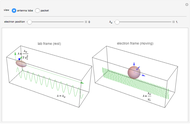
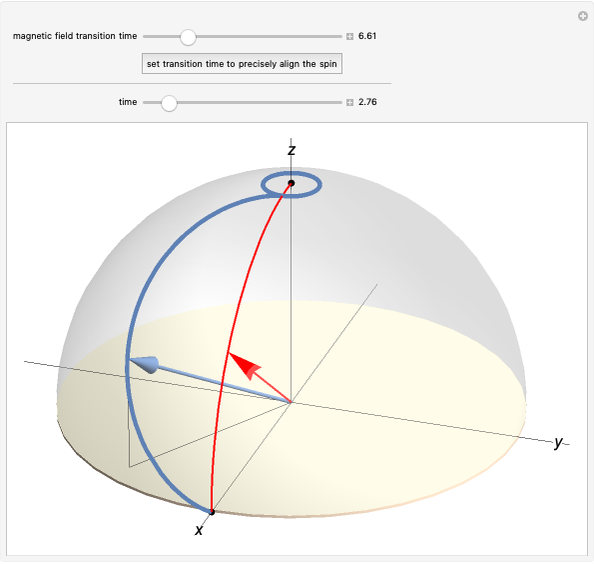
A particle with spin precesses around an applied magnetic field. This Demonstration simulates control of the direction of spin by a magnetic field. When the spin is used as a quantum bit (qubit), its quantum state corresponds to a point on the Bloch sphere shown. In that case, the control operation corresponds to the action of a single-qubit quantum gate.
Contributed by: Tad Hogg (June 2020)
Open content licensed under CC BY-NC-SA
Snapshots
Details
An electron spin can act as a qubit. The component of its spin vector along a specified direction (e.g. the  axis in this Demonstration) corresponds to the bit having a value of 0 or 1. More generally, a qubit can be in a superposition of 0 and 1. These superpositions correspond to points on the Bloch sphere, as described, for example, in Nielsen and Chuang [1].
axis in this Demonstration) corresponds to the bit having a value of 0 or 1. More generally, a qubit can be in a superposition of 0 and 1. These superpositions correspond to points on the Bloch sphere, as described, for example, in Nielsen and Chuang [1].
Quantum computers can alter qubit states through a sequence of operations. Some of these operations apply to just a single qubit and move the point on the Bloch sphere.
One implementation of such an operation uses a changing magnetic field. A spin has a magnetic moment and thus precesses around the direction of an applied magnetic field. This precession alters the superposition of the qubit and its corresponding point on the Bloch sphere. This Demonstration illustrates how a changing magnetic field alters a qubit whose state is initially along the 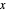 axis of the Bloch sphere. The magnetic field starts aligned with the direction of the spin, then changes uniformly to point along the
axis of the Bloch sphere. The magnetic field starts aligned with the direction of the spin, then changes uniformly to point along the  axis.
axis.
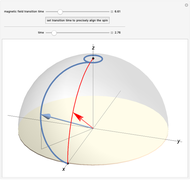
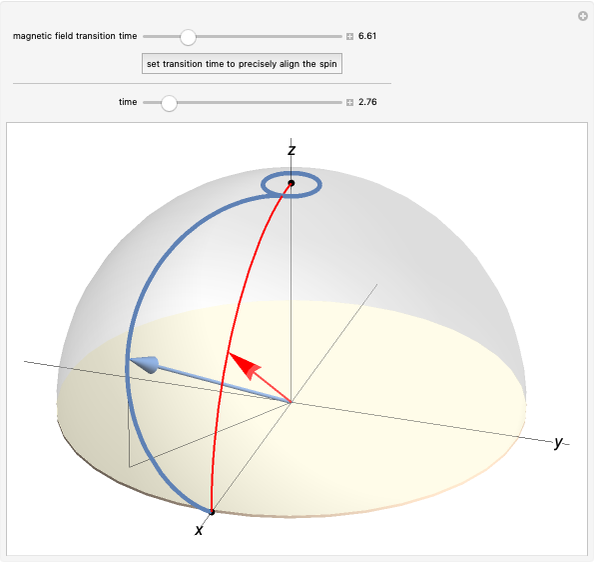
The top slider specifies the time over which the magnetic field changes its direction. The "set transition time to precisely align the spin" button sets the field transition time to a value that moves the spin to the  axis (see Snapshot 3). The thick blue curve shows the path of the spin vector on the sphere. The red curve is the path of the magnetic field.
axis (see Snapshot 3). The thick blue curve shows the path of the spin vector on the sphere. The red curve is the path of the magnetic field.
The bottom slider specifies the time since the start of the transition. As time changes, both the spin and magnetic field vectors move along the indicated paths. The arrows in the plot show these vectors at the time specified by the slider. Initially, both arrows are along the 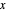 axis.
axis.
Snapshot 1: If the magnetic field changes slowly, the spin closely tracks the changing magnetic field. In this case, the spin's precession makes the spin alternate between being slightly ahead and slightly behind the changing field. In the limit of very slow changes (the so-called adiabatic limit), the spin is closely aligned with the  axis at the end of the operation.
axis at the end of the operation.
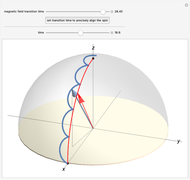
Snapshot 2: If the magnetic field changes too rapidly, the spin vector does not keep up with the change. Instead, the spin shifts only slightly from the 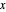 axis by the time the magnetic field finishes its change. After that, the spin precesses around the new direction of the magnetic field—that is, the
axis by the time the magnetic field finishes its change. After that, the spin precesses around the new direction of the magnetic field—that is, the  axis.
axis.
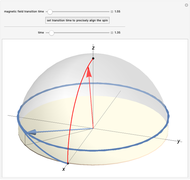
Snapshot 3: With a finely tuned choice of an intermediate rate of magnetic field change, the spin arrives at the  axis at the same time as the magnetic field. During the transition, the spin direction deviates from that of the magnetic field.
axis at the same time as the magnetic field. During the transition, the spin direction deviates from that of the magnetic field.
Reference
[1] M. A. Nielsen and I. L. Chuang, Quantum Computation and Quantum Information, New York: Cambridge University Press, 2000.
Permanent Citation