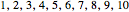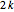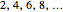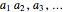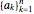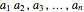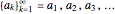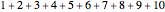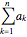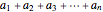Sequence and Summation Notation

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
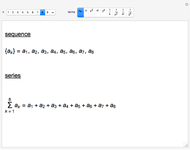
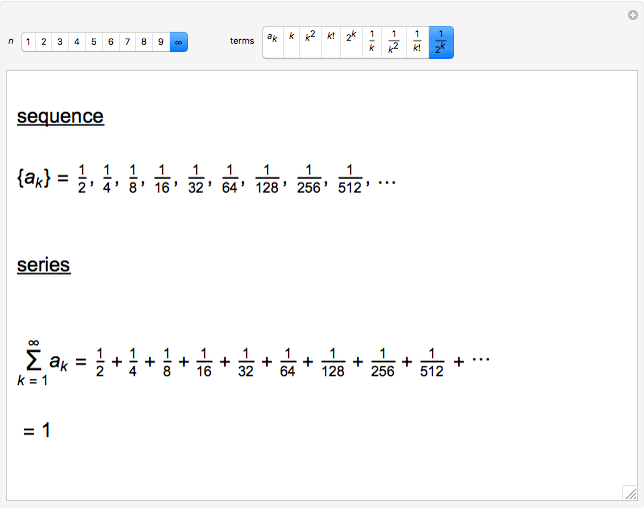
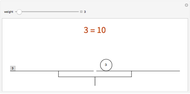
A sequence is an ordered set of numbers 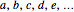 that may have a finite or infinite number of terms. If the sequence is finite, the last term is shown, like
that may have a finite or infinite number of terms. If the sequence is finite, the last term is shown, like 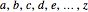 .
.
Contributed by: S. M. Blinder (July 2018)
Open content licensed under CC BY-NC-SA
Snapshots
Details
A finite series always has a sum: just add up the terms. Formulas for two basic finite series are

and
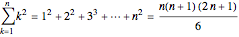 .
.
An infinite series may or may not have a finite sum.
The partial sums of an infinite series  are the sequence
are the sequence 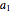 ,
, 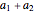 ,
, 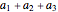 , …. If the sequence of partial sums has a limit, that is called the sum of the series.
, …. If the sequence of partial sums has a limit, that is called the sum of the series.
The partial sums may grow without bound, like for the series 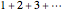 . Then the sum is infinite and the symbol
. Then the sum is infinite and the symbol 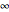 is used as if it were a number, like this:
is used as if it were a number, like this:
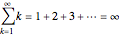 .
.
Even if the terms get smaller, the partial sums may still grow without bound as more terms are added. For example,
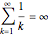 .
.
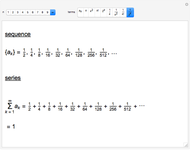
An infinite series may have a finite sum, but the terms must get small quickly enough. Any decimal is the sum of an infinite series: the powers of 10 in the denominators grow so quickly. For example,
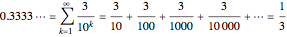 .
.
Permanent Citation