3D Rep-Tiles and Irreptiles

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
This Demonstration generalizes the topic of rep-tiles and irreptiles to the third dimension.
[more]
Contributed by: Karl Scherer (November 2012)
Additional contribution: David Sicherman
Open content licensed under CC BY-NC-SA
Snapshots
Details
Introduction
The search for 3D rep-tiles and 3D irreptiles at first brings up only very straightforward examples, which you will find shown as the first eight tilings:
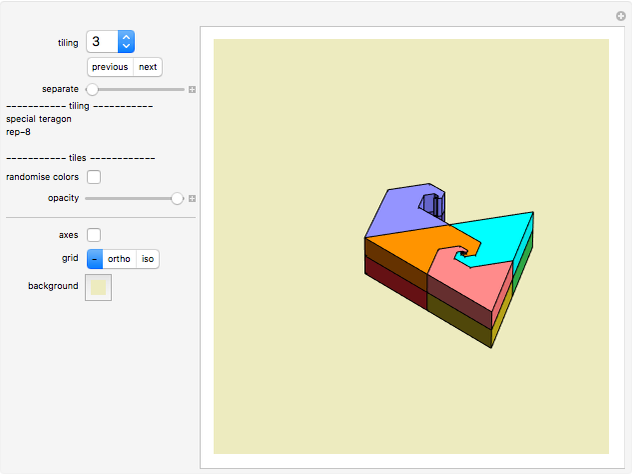
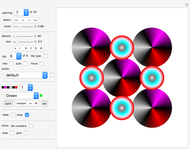
Tiling 1: any prism is a 3D rep-8. Tiling 2: special 3D rep-8. Tiling 3: extruded teragon is 3D rep-8 (a teragon is a polygon with an infinite number of sides). Tiling 4 and 5: the cube (and any cuboid) is a 3D rep-8. Tiling 6: the L-tricube is a 3D rep-8. Tiling 7: the L-tetracube is a 3D rep-8. Tiling 8: the P-pentacube is a 3D rep-8.
We can clearly see a pattern here: in each case, a two-dimensional tiling has been used and simply expanded to the third dimension by giving the tiles a unit thickness and then layering two of these expanded tilings on top of each other.
Thus a 2D rep-4 is used to create a 3D rep-8. Similarly, a 2D rep-9 gives us a 3D rep-27 (see tiling 9) and a 2D rep- gives us a 3D rep-
gives us a 3D rep- , where
, where 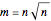 , so that the layering method only works if the square root of
, so that the layering method only works if the square root of  is an integer.
is an integer.
This is illustrated in tiling 10: an isosceles right triangle can be tiled by two smaller copies, but placing one of these layers of prisms on top of the other does NOT make an irreptile, because the resulting large prism should have a thickness that is not twice that of the smaller parts, but should differ in thickness by a factor of the square root of two, which is impossible.
This proves that not all two-dimensional regular tilings have a three-dimensional counterpart.
Simple Irregular 3D Tilings
If we further tile one of the 3D-tiles in a rep-8 tiling into eight smaller parts we obtain an irregular tiling, which shows that each rep-8 is also an irrep-15. This has been executed for the cube; see tiling 5.
Definitions
For a given two- or three-dimensional shape, let "rep-order" denote the smallest possible rep-number and "irrep-order" denote the smallest possible irrep-number for this shape.
We call an "extrusion" any 3D object that is created from a 2D shape by giving it some thickness.
Challenges Ahead
The question arises whether there are more interesting examples of 3D irreptiles than just the layering of tilings that are known from two-dimensional irreptiles.
Six challenges (with increasing difficulty) immediately come to mind:
Challenge 1: find a self-tiling of a 3D irreptile that is not layered.
Challenge 2: find a 3D irreptile whose most simple self-tiling is not layered. To be precise: find a 3D irreptile whose set of most simple self-tilings does not contain a tiling that consists of several layers of copies of a "thickened" 2D tiling.
Challenge 3: is there a 2D shape that is not a rep-tile, but whose 3D extrusion is a rep-tile?
Challenge 4: find a 3D irreptile that has a regular tiling and for which irrep-order < rep-order. In two dimensions, these cases abound. In three dimensions, it is not obvious whether such cases exist.
Challenge 5: find a 3D irreptile which does not have a regular tiling. In two dimensions many irreptiles do not have a regular self-tiling. It is not obvious whether in 3D such cases exist at all.
Challenge 6: find a 3D irreptile with a finite number of faces which is not a 3D rep-tile.
Solution to Challenge 1
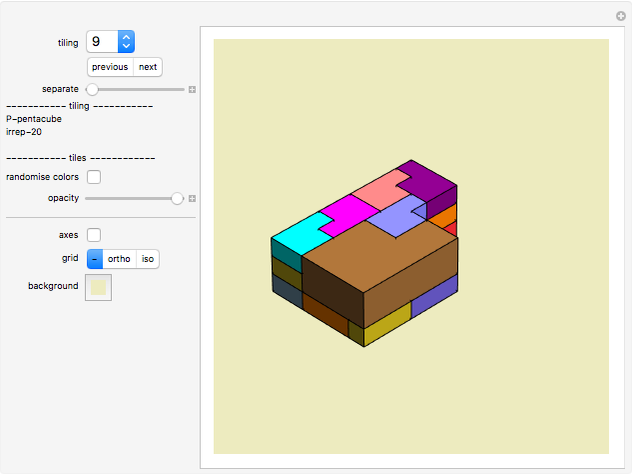
Tiling 9 gives us a solution: we could have created a two-dimensional regular tiling of the P-pentacube with nine pieces of the same size, and we could have layered three of these tilings to create a 3D rep-27 tiling. Instead, we have replaced some of these tiles by a bigger tile, and we end up with a 3D irrep-20 tiling (note that the P-pentacube is not rep-20).
Here we used the third dimension for a somewhat unusual tiling. However, it is not a solution to Challenge 2 because the most simple self-tiling is still layered. And it is not a solution to Challenge 3 because it does not reduce the minimum number of pieces (rep-order = 8).
Solution to Challenge 2
There are infinitely many solutions. We simply dissect an 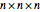 cube (where
cube (where  is an integer) into two congruent tiles with a thickness of at least 2 in each direction. This ensures that there cannot be any layers of thickness 1.
is an integer) into two congruent tiles with a thickness of at least 2 in each direction. This ensures that there cannot be any layers of thickness 1.
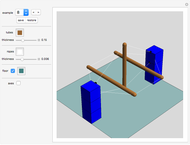
Tilings 11 and 12 shows the most simple example: two copies of the special tetracubes tile a 2×2×2 cube, hence eight copies tile a large version of the tetracube.
Solution to Challenge 3
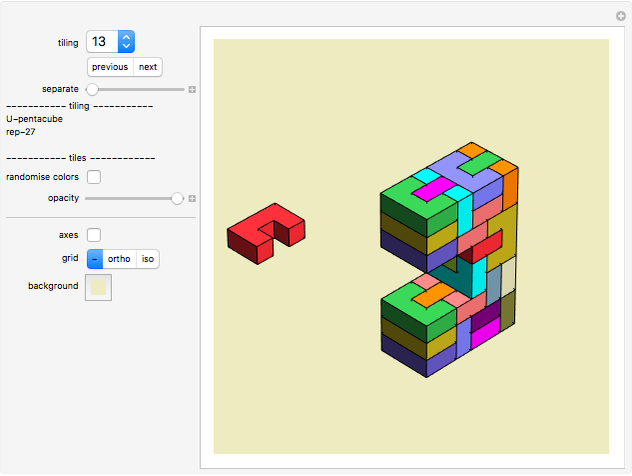
The U-shaped pentacube shown in tiling 13 is one of many 3D irreptile solutions. The associated 2D pentasquare is not a rep-tile. It is not even an irreptile, but its extrusion of thickness 1 is a 3D rep-tile.
Even very simple 3D irreptiles can have a very high rep-order.
Unsolved: amongst the solutions to Challenge 3, which is the one with the smallest irrep-order?
Unsolved: amongst the solutions to Challenge 3, which is the one with the smallest rep-order?
Tiling 15 shows how eight copies of a C-hexacube tile a 2×4×6 brick. Thirty such bricks tile a 12×12×12 cube, which contains 288 tiles. Six such cubes tile a large C-pentacube, hence it is a rep-1728.
However, we can do better: we observe that nine bricks (containing eight C-hexacubes each) tile a 6×6×12 dicube, three copies of which tile the C-hexacube. Hence it is a rep-216.
The same is true for the 3D pentacube "worm" displayed in tiling 16.
Tiling 16 shows a 3D pentacube which is rep-250.
Solutions to Challenge 4 Tiling 31 shows the most simple solution (by David Sicherman). The b-shaped heptacube is irrep-20 (shown) and rep-27 (proof left to the reader). Furthermore, the C-shaped hexacube is irrep-57 and rep-64. Can you find the associated tilings? The L-shaped pentacube is irrep-38 and rep-64. Can you find the associated tilings?
Is there a solution to challenge 4 that is irrep-n with n < 20 ? (unsolved)
Solutions to Challenge 5
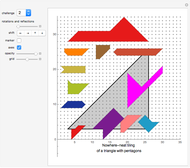
Tilings 17 and 18 show two examples that are irrep-22. Note that each tile has an infinite number of faces. The tiles are 2D teragons extruded into 3D. Each 2D teragon tiles a regular triangle with two copies of different sizes. (A teragon is a polygon with an infinite number of sides).
Similarly, an infinite number of solutions can be created which are irrep-30, irrep38, irrep-46 etc. To find those, we start with a regular triangle with side length 1 which is cut into two similar teragons, one much bigger than the other. The larger teragon always has the base length of 1. If the smaller copy has base length 1/3, then its 3D extrusion is irrep-30. If the smaller teragon's base length is 1/4, then its 3D extrusion is irrep-38.
Tilings 19, 20 and 21 show more objects that are irrep-22. All of them have an infinite number of faces.
We can also start with a trisection of a regular triangle into three similar teragons, the second one half the size of the first, and the third half the size of the second. This results in an irrep-50 irreptile (see tiling 22).
Solutions to Challenge 6
It is somewhat surprising that there are solutions to this challenge at all.
The author has found only seven solutions. They are shown in tilings 23 to 30. Can you find more examples?
Tiling 30 is only an indicated solution here because of the large number of tiles (452) needed. The reader can easily deduce from this 2D diagram how the extruded 3D object is tiled with smaller copies of itself (use 2 layers of the two largest tiles, 4 layers of the intermediary tiles and 12 layers of the small tiles).
Hint
Remember that you can always zoom in and out with CTRL+Mouseshift.
Technical Remark regarding the Use of the Mathematica Command "Polygon"
The 3D tilings in this Demonstration show polycubes and other 3D objects.
In the program each tile is described only once. There a 3D tile is (very conveniently) defined as a Polygon, and a Polygon is given as a set of sets of points (the "collection of walls" of the 3D object, so to speak), which can then be translated, rotated, and enlarged as one object using the Mathematica commands Translate, Rotate, and Scale to place these 3D objects in the various positions where they should be in the tiling and to size them as desired.
This use of the term Polygon as a Mathematica command is different from the usual meaning of a polygon in mathematics, defined as a single set of vertices that describe one two-dimensional object.
History
David Sicherman found quite a few pentacubes and hexacubes that are rep-n of low order n, see page 13 as an example (the u-pentacube is rep-27). He also found a few polycubes with irrep-number smaller that rep-number (see challenge 4 above).
Permanent Citation