Briggs-Rauscher Mechanism: The Chemical Color Clock

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
The reactions involved in the Briggs–Rauscher (BR) mechanism are the following:
[more]
Contributed by: Housam Binous and Brian G. Higgins (April 2011)
Open content licensed under CC BY-NC-SA
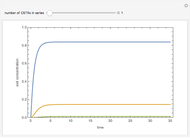
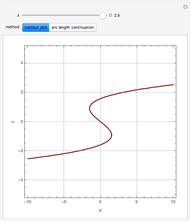
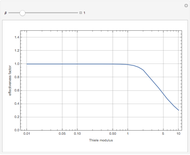
Snapshots
Details
The members of the sequence  are the compositions of
are the compositions of  , respectively. The concentration of
, respectively. The concentration of  is taken as a constant equal to
is taken as a constant equal to  . In the program, the symbols
. In the program, the symbols  , K1, K2, …, and k1, k2, … are the different rate constants and constants appearing in the rate laws (see [1] for details).
, K1, K2, …, and k1, k2, … are the different rate constants and constants appearing in the rate laws (see [1] for details).
In the program, X10, X20, …, X100 are the 10 concentrations of the various components in the feed stream of the open reactor. The reactor’s residence time equal to  ; the Mathematica variable A is a constant equal to
; the Mathematica variable A is a constant equal to  .
.
References
[1] P. De Kepper and I. R. Epstein, "A Mechanistic Study of Oscillations and Bistability in the Briggs–Rauscher Reaction," Journal of the American Chemical Society, 104(1) , 1982 pp. 49–55.
, 1982 pp. 49–55.
[2] M. M. Thomas, "The Briggs–Rauscher Reaction: Chemistry Clock in Color," Mathematica in Education and Research, 11(1), 2006 pp. 129–137.
Permanent Citation