The Effects of Coinsurance and Deductibles on Optimal Precautions for Weibull-Distributed Loss

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
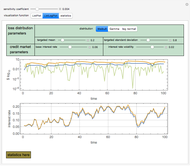
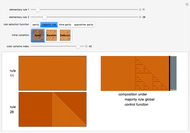
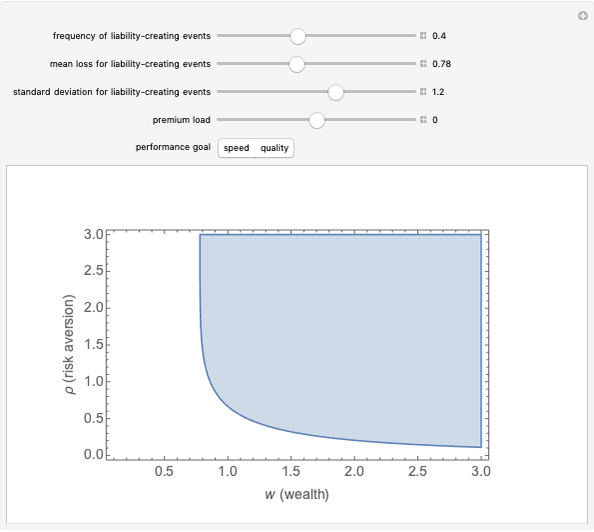
This Demonstration examines the effects of coinsurance and deductibles on optimal precautions for Weibull-distributed losses, such as those frequently used to model hurricanes, earthquakes, and other catastrophes. The issue is important because regulation of deductibles and coinsurance mediates two dueling goals. One goal is to provide insureds and those who depend on them with fairly complete insurance. A second goal, however, is to protect the public, who often backstop catastrophe insurance schemes, from precaution-decreasing moral hazard likely to result when insurance is very complete. Thus, in assessing the virtue of regulations requiring heightened deductibles and coinsurance, it is important to consider the magnitude of loss reductions likely to result: the greater the effect, the stronger the case for regulation. This Demonstration estimates such magnitudes based on a theoretical model of insured behavior.
[more]
Contributed by: Seth J. Chandler (December 2012)
With additional contributions by: Oleksandyr Pavlyk
Open content licensed under CC BY-NC-SA
Snapshots
Details
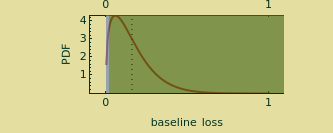
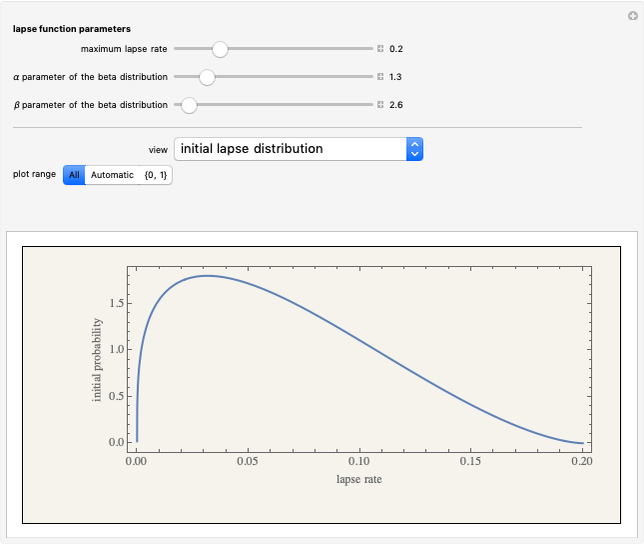
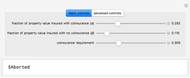
The model underlying this Demonstration assumes that catastrophic events, when they occur, create losses that obey a Weibull distribution. This distribution is calibrated such that a materialization of 1 means that the losses equal the value of the property. A high percentage of the time, however, no losses occur at all. For payment of an amount 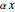 , the insured may take precautions against loss that reduce the size of any baseline loss
, the insured may take precautions against loss that reduce the size of any baseline loss  to an amount
to an amount 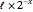 , such that the size of the loss is reduced by one half for each marginal unit of precautions. Thus, if
, such that the size of the loss is reduced by one half for each marginal unit of precautions. Thus, if  is the deductible and
is the deductible and  is the rate of coinsurance, the actual loss suffered by the insured from precautions and any loss
is the rate of coinsurance, the actual loss suffered by the insured from precautions and any loss  , after consideration of insurer payments, is
, after consideration of insurer payments, is 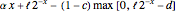 . If
. If 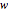 is the probability of a catastrophic event occurring, the distribution of losses suffered by the insured may be written as a mixture distribution in which (1) the first component is always zero (no loss); (2) the second component is a transformed Weibull distribution conditioned on the loss's being less than the deductible (the transformation is
is the probability of a catastrophic event occurring, the distribution of losses suffered by the insured may be written as a mixture distribution in which (1) the first component is always zero (no loss); (2) the second component is a transformed Weibull distribution conditioned on the loss's being less than the deductible (the transformation is 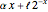 ); and (3) the third component is a transformed Weibull distribution conditioned on the loss's being greater than the deductible (the transformation is
); and (3) the third component is a transformed Weibull distribution conditioned on the loss's being greater than the deductible (the transformation is 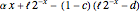 ).
).
The CDF of this mixture distribution may be written as:
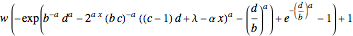 if
if 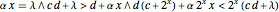 ;
;
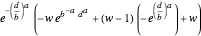 if
if 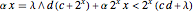 ;
;
 if
if 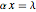 ;
;
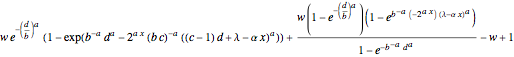 if
if 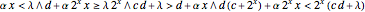 ;
;
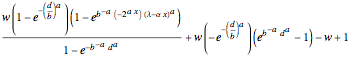 if
if 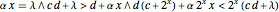 ;
;
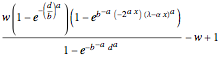 if
if 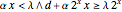 ;
;
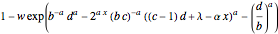 if
if 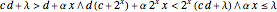 ;
;
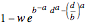 if
if 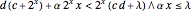 ;
;
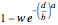 if
if 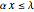 ;
;
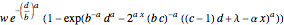 if
if 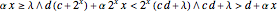 ;
;
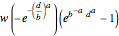 if
if 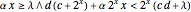 ;
;
 if
if 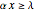 ;
;
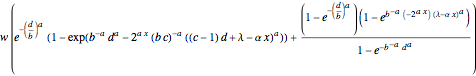 if
if 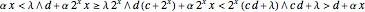 ;
;
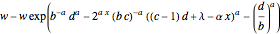 if
if 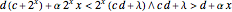 ;
;
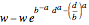 if
if 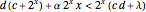 ;
;
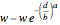 otherwise.
otherwise.
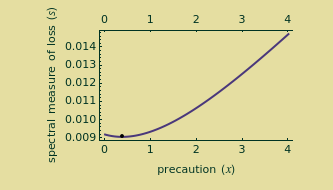
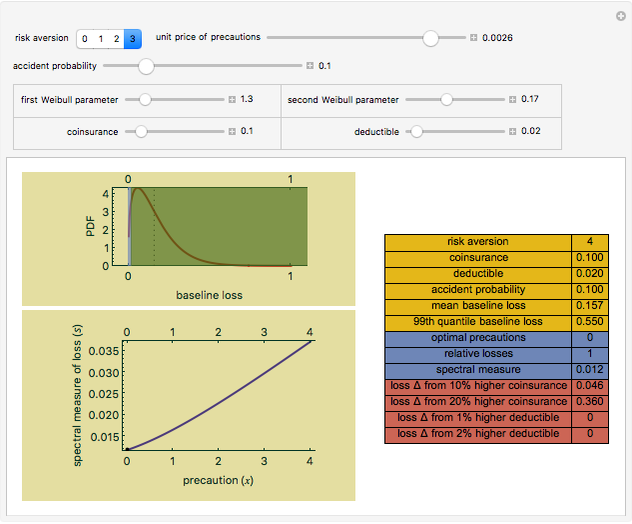
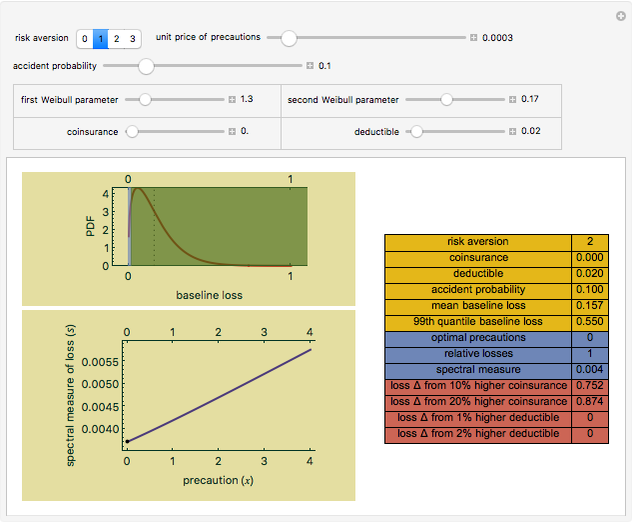
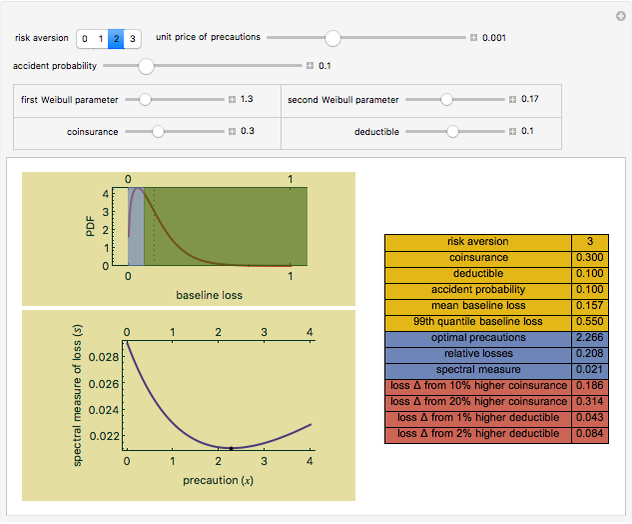
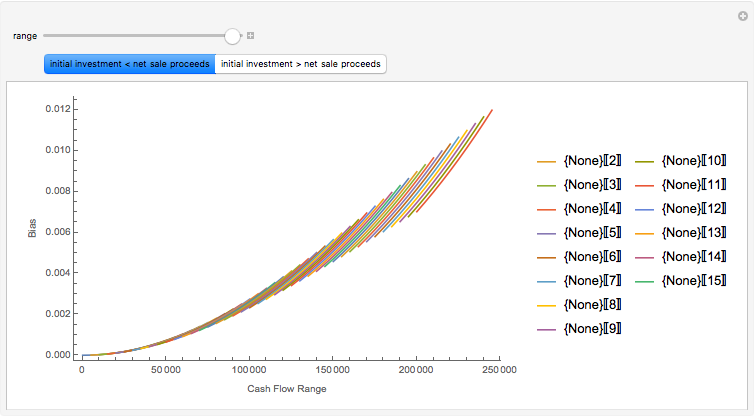
You can then compute the expected quantile of this outcome mixture distribution subject to a weighting function that is nondecreasing in losses and whose domain is the interval 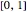 . The spectral measure approach to risk, coupled with an assumption of rational behavior on the part of the insured, permits you to determine the optimal level of precautions by the insured by finding the value of precautions
. The spectral measure approach to risk, coupled with an assumption of rational behavior on the part of the insured, permits you to determine the optimal level of precautions by the insured by finding the value of precautions  that minimizes this expectation. It is this relationship between precautions
that minimizes this expectation. It is this relationship between precautions  and spectral measure that is displayed on the graphic above.
and spectral measure that is displayed on the graphic above.
It turns out that a closed-form solution to the expected quantile is difficult or impossible to obtain. However, as noted by Oleksandr Pavlyk, an expected quantile is equivalent to the expectation of a random variable 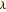 multiplied by a special probability density function, where
multiplied by a special probability density function, where 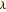 is drawn from the outcome distribution. The special probability density function is the PDF of the weighting function evaluated at the CDF of the outcome distribution when in turn evaluated at
is drawn from the outcome distribution. The special probability density function is the PDF of the weighting function evaluated at the CDF of the outcome distribution when in turn evaluated at 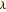 . With this method, you can obtain the following closed forms for expected quantile.
. With this method, you can obtain the following closed forms for expected quantile.

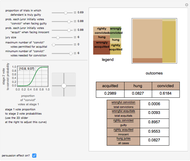
By differentiating these spectral measures with respect to  and then bounding the results between 0 and some arbitrarily large value, you can then obtain the optimal level of precautions. The table below shows closed-form values.
and then bounding the results between 0 and some arbitrarily large value, you can then obtain the optimal level of precautions. The table below shows closed-form values.

Often when you work with spectral measures, you use a weighting function that is nonincreasing rather than one, as here, that is nondecreasing. A nonincreasing weighting function is used here, however, because the underlying outcome is a loss. Risk aversion thus requires that the larger losses be weighted at least as heavily as the smaller losses.
Although the discussion in this Demonstration focuses on insurance against catastrophes, the mathematics underlying it permits its extension to all sorts of insurable losses, provided they are Weibull distributed.
This Demonstration achieves its speed of computation through extensive use of the Mathematica compiler.
Snapshot 1: when the cost of precautions is high, the effect of greater deductibles and coinsurance is small, even when the insured is highly risk averse
Snapshot 2: when the cost of precautions is low, greater deductibles and coinsurance have an enormous effect on expected losses, even when the insured is not particularly risk averse
Snapshot 3: high deductibles and coinsurance result in high levels of optimal precautions
Some literature examining the use of the Weibull distribution in modeling catastrophe losses includes [1–5].
References
[1] C. Watson and M. Johnson, "Hurricane Loss Estimation Models: Opportunities for Improving the State of the Art," Bulletin of the American Meteoreorological Society, 85(11), 2004 pp. 1713–1726. journals.ametsoc.org/doi/pdf/10.1175/BAMS-85-11-1713.
[2] R. Hogg and S. Klugman, Loss Distributions, New York: Wiley, 1984.
[3] C. Kleiber and S. Kotz, Statistical Size Distributions in Economic and Actuarial Sciences, Hoboken, NJ: Wiley, 2003.
[4] W. K. Härdle and B. L. Cabrera, "Calibrating CAT Bonds for Mexican Earthquakes," Journal of Risk and Insurance, 77(3), 2010 pp. 625–650. doi:10.1111/j.1539-6975.2010.01355.x.
[5] M. Legg, L. Nozick, and R. Davidson, "Optimizing the Selection of Hazard-Consistent Probabilistic Scenarios for Long-Term Regional Hurricane Loss Estimation," Structural Safety 32(1), 2010 pp. 90–100. doi:10.1016/j.strusafe.2009.08.002.
Permanent Citation