The Persuasion Effect: A Traditional Two-Stage Jury Model

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
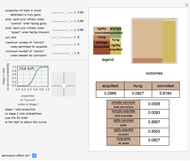
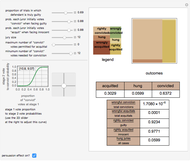
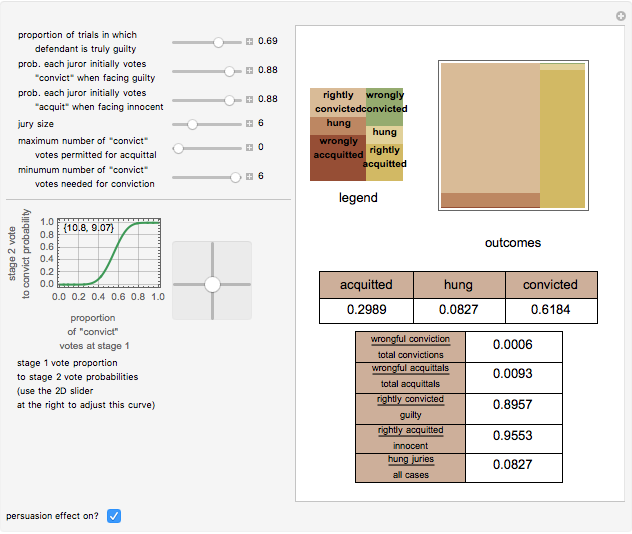
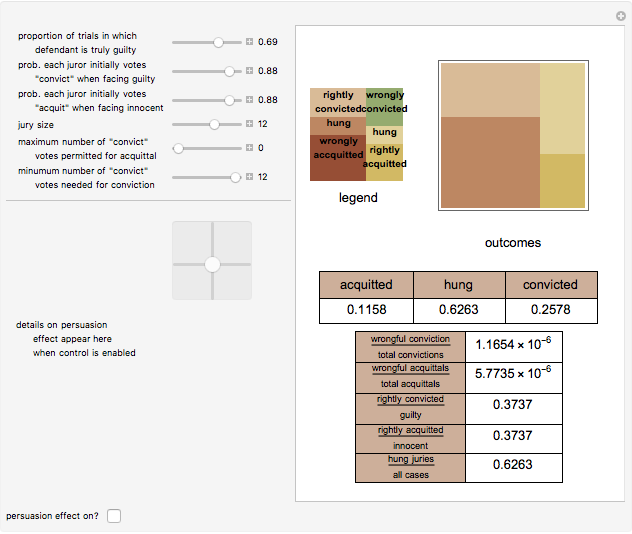
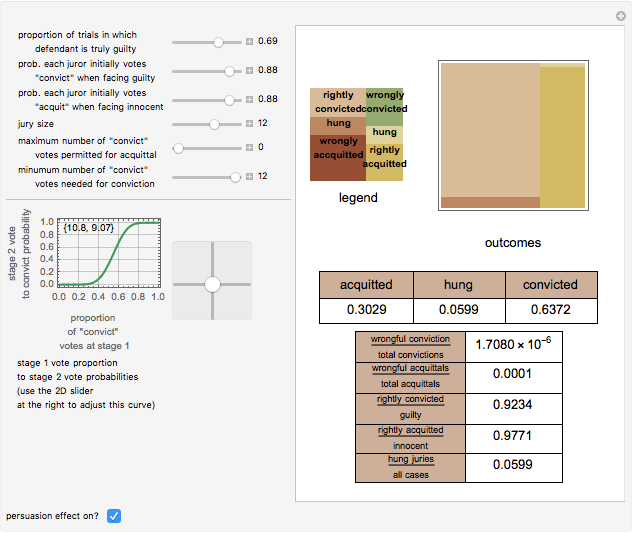
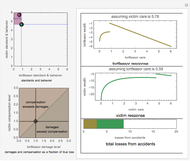
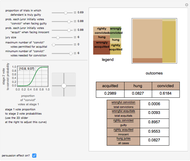
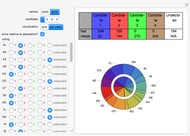
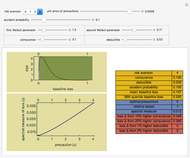
An influential model of jury behavior in American criminal cases suggests that in an initial stage jurors vote independently on the guilt or innocence of the defendant and that, in a second "persuasion stage," the outcome of that vote will affect the probable final distribution of votes to acquit or convict. Thus the following factors yield various statistics about the behavior of the jury system: (1) the incidence of guilt among those tried, (2) the probability that the jury will convict a "truly guilty" defendant, (3) the probability that the jury will acquit a "truly innocent" defendant, (4) a mapping between the distribution of initial vote and final vote (the "persuasion effect") and (5) an "outcome mapping" (legal rules determining the types of final votes that result in the conviction of the defendant, the acquittal of the defendant, or a so-called "hung jury").
[more]
Contributed by: Seth J. Chandler (July 2007)
Suggested by: Aaron Bruhl
Based on work by: Alan Gelfand, Herbert Solomon, and others
Open content licensed under CC BY-NC-SA
Snapshots
Details
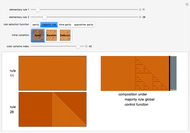
This model tends to produce quite low rates of wrongful conviction and wrongful acquittal even if individual juror accuracy is not terribly high. This finding may be seen as an artifact of (a) the assumption that the initial votes of the jurors are independent coupled with (b) the "persuasion effect" that, unless parameters are set in a way believed at odds with empirically determined behavior, tends to move final voting tallies towards polar extremes (almost all votes to convict or almost all votes to acquit) and thus wrings "hung juries" out of the system. If, however, jurors can be systematically misled or are systematically biased in at least certain types of cases then the binomial model used to generate the initial votes overestimates the number of independent jurors. Under these circumstances, the model is not appropriate and the outcomes will thus be inaccurate.
The model makes clear the importance of prosecutorial judgment in the outcome of criminal trials. The more innocent defendants the prosecutor brings to trial, the greater the probability that juror error will result in the conviction of innocent defendants. Nonetheless, an interesting feature of this model is its resilience to prosecutorial error. Even high proportions of trials of innocent defendants will not result in many wrongful convictions, at least so long as jurors do not wrongly convict innocent defendants too frequently. The model also allows you to see the effects of different legal rules regarding jury size and unanimity—a matter of interest to legal scholars and reformers.
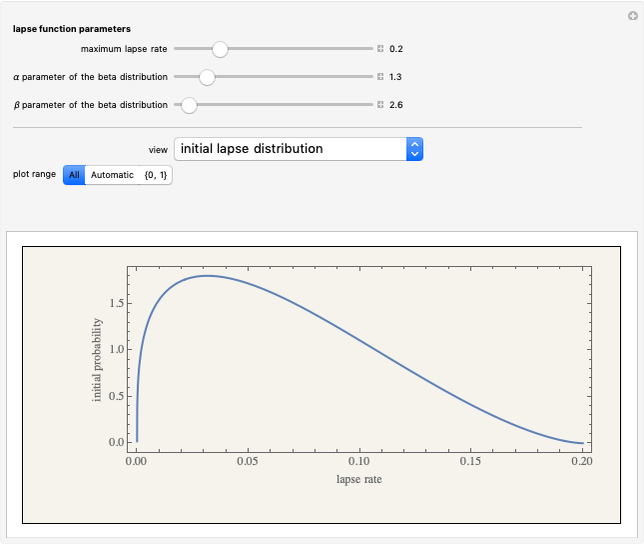
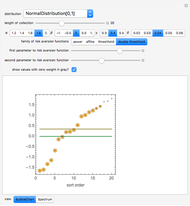
The persuasion stage is modeled by applying the cumulative distribution function of a user-selected beta distribution to the initial proportion of votes to convict. There is nothing "magic" about a beta function. It is selected because it has the right domain of [0,1] and because it can assume a broad variety of shapes depending on the parameters selected.
Exposition of this sort of model may be found in Gelfand and H. Solomon, "Considerations in Building Jury Behavior Models and in Comparing Jury Schemes: An Argument in Favor of 12-Member Juries," Jurimetrics Journal, 17, 1976 pp. 292-313.
Snapshot 1: Reducing the jury size to 6. Note the minimal effect on statistics of interest.
Snapshot 2: Turning the persuasion effect off. Notice the much higher rate of hung juries.
Snapshot 3: Showing the effect of prosecutions of large numbers of innocent defendants. Notice that while convictions decrease substantially, wrongful convictions do not increase substantially under this model.
Snapshot 4: Prosecution-biased persuasion in which even a low number of votes to convict in the initial vote leads to a large number of final votes to convict (a substantial percentage of which are wrongful) in the second stage.
Snapshot 5: A hypothetical system in which there are six jurors and in which four votes are needed for conviction, otherwise the defendant is acquitted. Note that the rate of wrongful conviction does not skyrocket under this system and that the cost of hung juries is eliminated.
Snapshot 6: A hypothetical system in which there are six jurors and in which four votes are needed for conviction, otherwise the defendant is acquitted. There is prosecution-biased persuasion in which even a low number of votes to convict in the initial vote leads to a large number of final votes to convict (a substantial percentage of which are wrongful) in the second stage.
Permanent Citation
"The Persuasion Effect: A Traditional Two-Stage Jury Model"
http://demonstrations.wolfram.com/ThePersuasionEffectATraditionalTwoStageJuryModel/
Wolfram Demonstrations Project
Published: July 30 2007