Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Evidentiary Uncertainty

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

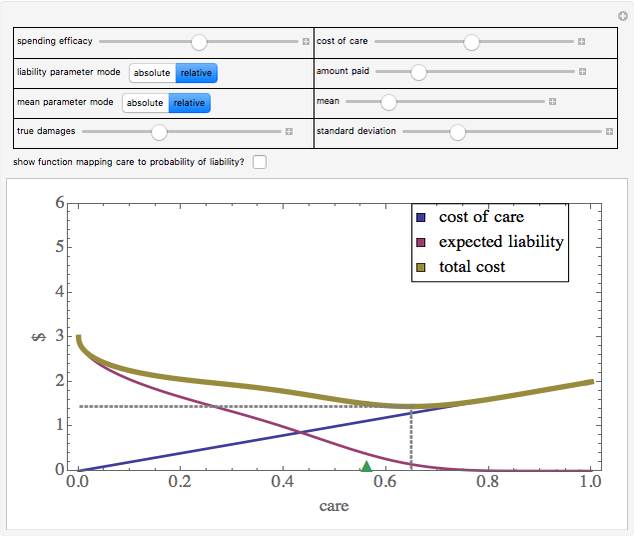
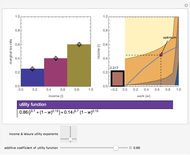
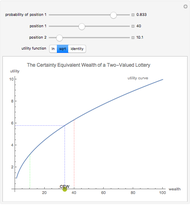
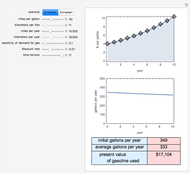
One can often realistically model the likelihood that an entity will be held to have violated some standard as a monotonically decreasing function of the amount of care that person took to avoid harm. Models of this sort are sometimes referred to as exhibiting "evidentiary uncertainty". An example might be liability under the common law "negligence" system in which the more care an individual took the less likely a court or jury is to find them liable for injuries that resulted from their actions.

[more]

This Demonstration determines the rational behavior one should expect to see under such a system. There are a number of controls that determine the outcome.

"Spending efficacy" determines the relationship between an amount spent on care and the probability of an accident.

"Cost of care" sets the marginal cost of care.

Two related controls determine the damages the entity may have to pay. When its corresponding "mode" control is set to "absolute", the control for amount paid directly determines how much the entity will have to pay in the event the entity is found liable. When its corresponding "mode" control is set to "relative", the control for amount paid indirectly determines how much the entity will have to pay in the event the entity is found liable. It does so by making the amount to be paid the value of the control multiplied by the true damages created by the accident.

Three related controls determine the relationship between the amount of care taken and the probability that the entity will be found liable (or not liable) in the event of an accident. The concept is to set the probability of being found not liable as the CDF of a beta distribution. You determine which particular beta distribution will be used by moving the controls to affect the mean and standard deviation of that distribution. When its corresponding "mode" control is set to "absolute", the mean control directly sets the mean of the distribution. When its corresponding "mode" control is set to "relative", the mean control indirectly sets the mean of the distribution by making the mean a multiple of the value of the control and the "efficient" level of care. "Efficient" in this context means the amount of care that would be taken by an entity seeking to minimize the total of actual expected accident costs (using true damages) and care costs. The standard deviation control sets the standard deviation of the distribution as a multiple of the maximum possible standard deviation given the already selected mean.

A final control determines whether the plot produced by the Demonstration should contain an informative inset.

The Demonstration responds with a plot showing the relationships (1) between care and the cost of care, (2) care and the expected liability of the entity, and (3) care and total costs (cost of care plus expected liability). It also shows with a dotted line the level of care that minimizes the entity's total cost and the associated minimum cost. It thus predicts the behavior one would expect to see from a fully informed and rational entity. A green triangle marks the "efficient" level of care, that is, the level of care that someone would take if they wanted to minimize the expected actual cost of an accident plus care costs. If the inset control is selected, the Demonstration also produces a graphic showing the relationship between care and (a) the probability of being found liable if an accident occurs and (b) the probability of an accident.

[less]

Contributed by: Seth J. Chandler (May 2009)
Open content licensed under CC BY-NC-SA

Snapshots

Details

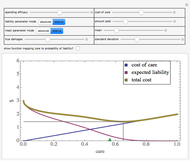
For simplicity, the marginal cost of care is set to a constant.

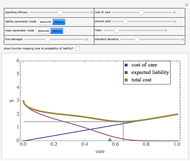
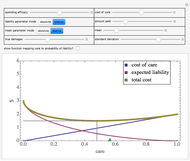
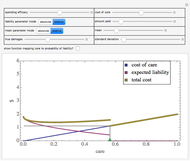
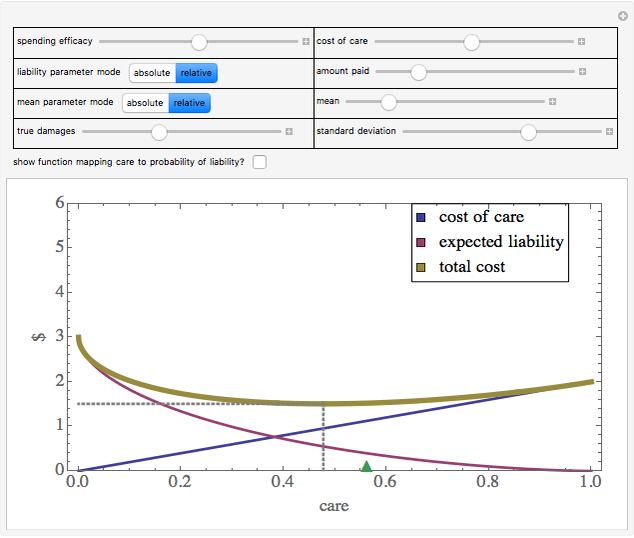
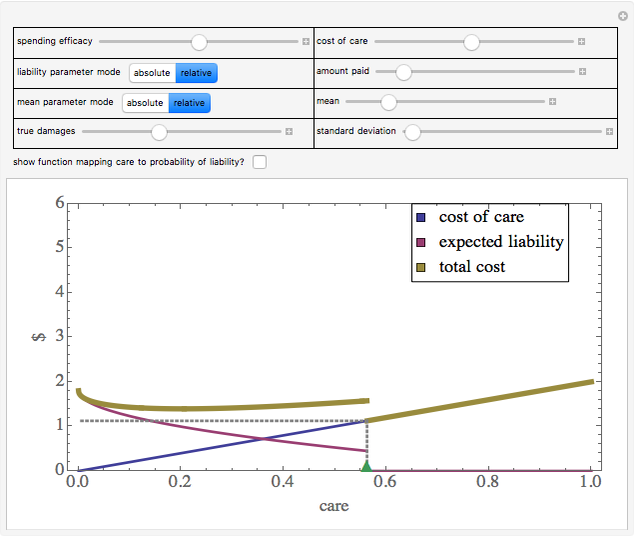
Snapshot 1: a somewhat inaccurate judicial system results in the entity taking more than efficient care

Snapshot 2: a highly inaccurate judicial system results in the entity taking less than efficient care

Snapshot 3: a highly accurate judicial system, coupled with the liability standard being set at the efficient level, results in the entity taking the efficient level of care even when the amount it has to pay if found liable is somewhat less than true damages

Snapshot 4: a highly accurate judicial system, coupled with the liability standard being set at the efficient level, results in the entity taking less than the efficient level of care when the amount it has to pay if found liable is much less than true damages

Snapshot 5: a somewhat inaccurate judicial system, coupled with the liability standard being set at the efficient level, results in the entity taking more than the efficient level of care even when the amount it has to pay if found liable is somewhat less than true damages

Snapshot 6: simulation of a "strict liability" system in which the entity is liable almost no matter what it does

An article bearing on this topic, along with a useful bibliography may be found in Yoon Ha Yoo, Does Evidentiary Uncertainty Induce Excess Injurer Care?

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send