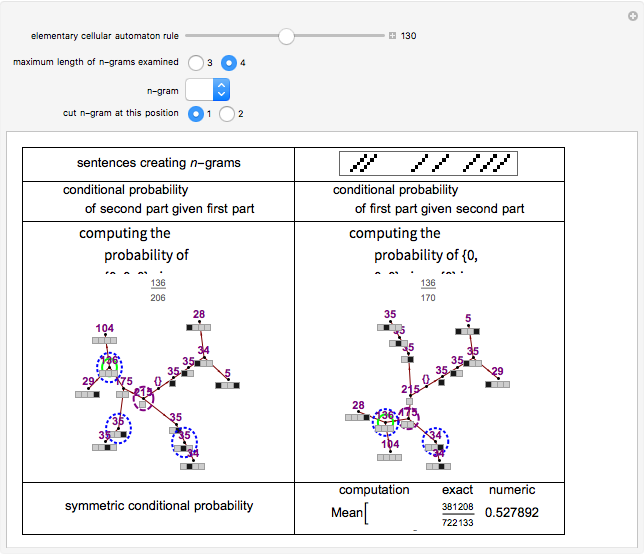
Collocation by Symmetric Conditional Probability

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
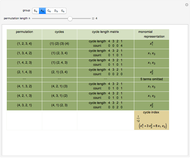
Roughly speaking, a "collocation" is an  -gram (subsequence) that appears more frequently in some sequence than would be expected if the constituent parts of the
-gram (subsequence) that appears more frequently in some sequence than would be expected if the constituent parts of the  -gram were drawn at random. One way of making this definition more precise is to use the notion of "symmetric conditional probability". For a bigram (i.e., an
-gram were drawn at random. One way of making this definition more precise is to use the notion of "symmetric conditional probability". For a bigram (i.e., an  -gram with two parts), its symmetric conditional probability is the product of (1) the conditional probability that the second half of the bigram would appear given the first half of the bigram and (2) the conditional probability that the first half of the bigram would appear given the second half of the bigram. Bigrams with high specific conditional probability may be thought of as collocations. This concept can be extended to
-gram with two parts), its symmetric conditional probability is the product of (1) the conditional probability that the second half of the bigram would appear given the first half of the bigram and (2) the conditional probability that the first half of the bigram would appear given the second half of the bigram. Bigrams with high specific conditional probability may be thought of as collocations. This concept can be extended to  -grams by cutting the
-grams by cutting the  -gram at all positions
-gram at all positions  (where
(where  is the length of the
is the length of the  -gram), finding the symmetric conditional probability of this "pseudo-bigram", and then taking the mean of the results.
-gram), finding the symmetric conditional probability of this "pseudo-bigram", and then taking the mean of the results.
Contributed by: Seth J. Chandler (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The Demonstration executes faster when the maximum length of  -grams examined is set to 3.
-grams examined is set to 3.
An application of the concept behind this Demonstration will be presented at the 2008 International Mathematica Symposium, where it will be used as part of an effort to find critical concepts in the leading international treaty governing sales of goods.
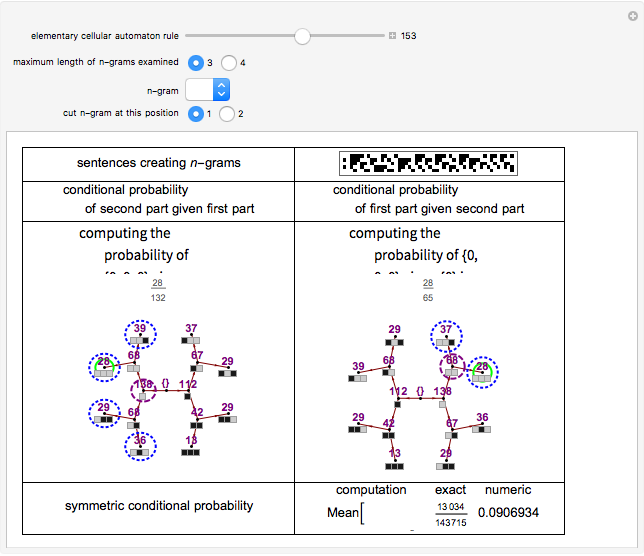
Snapshot 1: Examines the  -gram {0,0,0} in sentences generated by Rule 153. Slice position for creating the pseudo-bigram is 1.
-gram {0,0,0} in sentences generated by Rule 153. Slice position for creating the pseudo-bigram is 1.
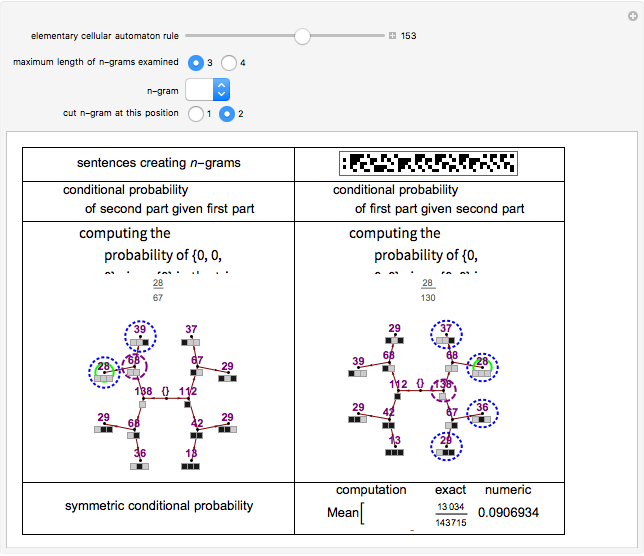
Snapshot 2: Examines the  -gram {0,0,0} in sentences generated by Rule 153. Slice position for creating the pseudo-bigram is 2.
-gram {0,0,0} in sentences generated by Rule 153. Slice position for creating the pseudo-bigram is 2.
Snapshot 3: Examines the  -gram {0,0,0} in sentences generated by Rule 130. Slice position for creating the pseudo-bigram is 1. It has a high symmetric conditional probability and could be a collocation.
-gram {0,0,0} in sentences generated by Rule 130. Slice position for creating the pseudo-bigram is 1. It has a high symmetric conditional probability and could be a collocation.
Permanent Citation