Dynamic Germination of Seeds and Microbial Spores

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
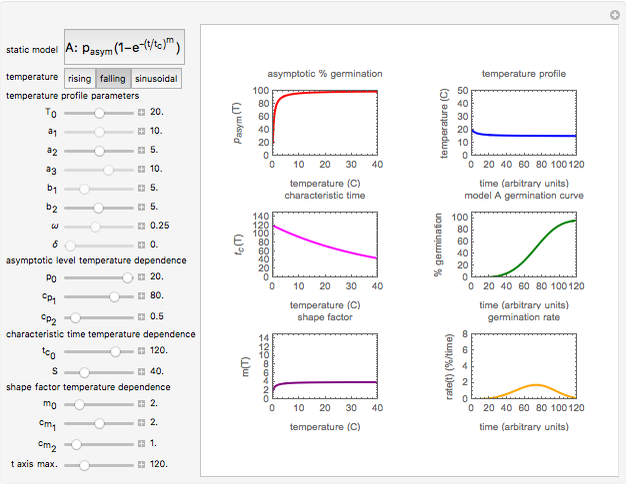
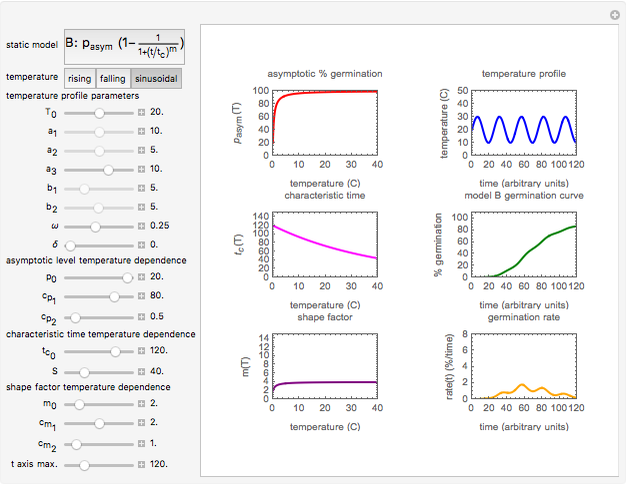
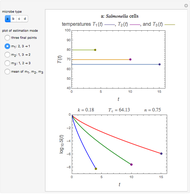
Models of the isothermal germination curves of plant seeds and bacterial, yeast, or fungal spores depend on three parameters representing the asymptotic germination level, a characteristic time, and the curve’s steepness or span. We assume that under non-isothermal conditions the momentary germination rate is the isothermal rate at the momentary temperature at a time that corresponds to the momentary germination level. If so, the isothermal models can be converted into a dynamic rate model whose coefficients are the temperature dependencies of the isothermal model parameters. This Demonstration lets you generate dynamic germination curves, both sigmoid and non-sigmoid, with two germination models for rising, falling, and oscillating (sinusoidal) temperatures.
Contributed by: Mark D. Normand, Murray Eisenberg, and Micha Peleg (July 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
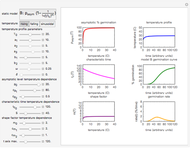
Snapshot 1: germination in rising temperature simulated with Model B
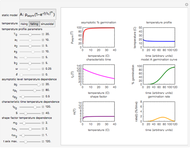
Snapshot 2: germination in falling temperature simulated with Model A
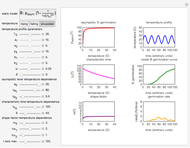
Snapshot 3: germination in oscillating temperature simulated with Model B
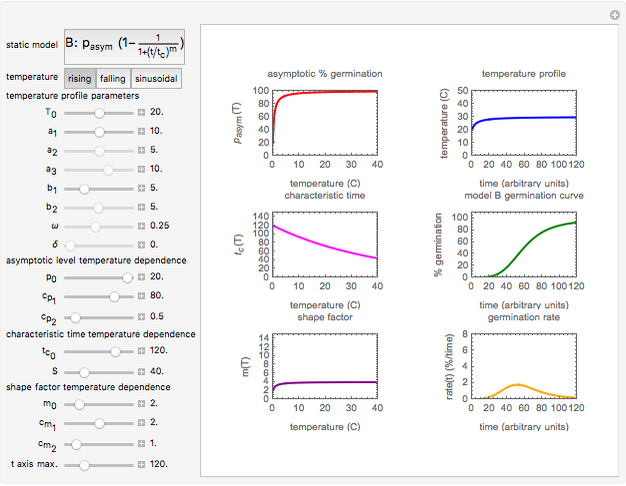
Snapshot 4: non-sigmoid germination in rising temperature simulated with Model A
 An isothermal germination curve is a plot of the percentage of germinated seeds or spores versus time recorded under static conditions. Its shape is usually but not always sigmoid. Such curves can be described mathematically by various models, of which we have chosen two, A:
An isothermal germination curve is a plot of the percentage of germinated seeds or spores versus time recorded under static conditions. Its shape is usually but not always sigmoid. Such curves can be described mathematically by various models, of which we have chosen two, A: 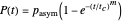 [1] and B: P(t)=pasym[1-1/(1+(t/
[1] and B: P(t)=pasym[1-1/(1+(t/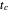 InlineMath)m)] [2], where
InlineMath)m)] [2], where 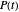 is the percent germination at time
is the percent germination at time  ,
, 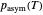 a temperature-dependent asymptotic germination level in percent,
a temperature-dependent asymptotic germination level in percent,  a temperature-dependent characteristic time in minutes, hours, or days, and
a temperature-dependent characteristic time in minutes, hours, or days, and 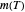 a dimensionless temperature-dependent "shape factor". (If
a dimensionless temperature-dependent "shape factor". (If 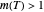 ,
, 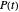 is sigmoid and if
is sigmoid and if 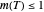 , it is non-sigmoid.)
, it is non-sigmoid.)
We assume that under non-isothermal conditions the momentary germination rate is the isothermal rate at the momentary temperature at a time that corresponds to the momentary germination level. Implementation of this assumption produces a dynamic rate model in the form of an ordinary differential equation (ODE) whose coefficients are composed of 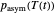 ,
, 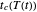 , and
, and 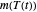 , where
, where 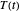 is the temperature history (or "profile"). This equation can be solved numerically to create the germination curve for a particular
is the temperature history (or "profile"). This equation can be solved numerically to create the germination curve for a particular 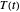 .
.
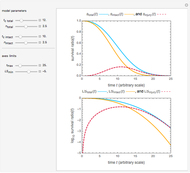
In this Demonstration, you can choose the germination model, A or B, and its parameters’ temperature dependence. There is a choice of three temperature profiles—rising, falling, and sinusoidal—whose characteristics can also be entered and modified. They are all in a temperature range where the temperature, presumably, accelerates and intensifies the germination. On the left side, the display includes plots of the temperature dependence of the three model parameters  ,
, 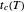 , and
, and 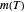 versus
versus 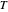 . On the right side are the chosen temperature profile
. On the right side are the chosen temperature profile  versus
versus  , the resulting dynamic germination curve
, the resulting dynamic germination curve 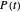 versus
versus  , and the germination rate versus
, and the germination rate versus  . Notice that if the parameter
. Notice that if the parameter  ,
, 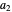 , or
, or 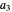 in the temperature profile's equation is set to zero, the Demonstration will generate an isothermal germination curve for the corresponding temperature
in the temperature profile's equation is set to zero, the Demonstration will generate an isothermal germination curve for the corresponding temperature 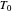 . Isothermal germination curves, however, can be generated much faster with an algebraic model as described in "Isothermal Germination of Seeds and Microbial Spores".
. Isothermal germination curves, however, can be generated much faster with an algebraic model as described in "Isothermal Germination of Seeds and Microbial Spores".
The Demonstration’s aim is only to present the concept and method. Thus, no effort has been made to simulate the germination pattern of any particular seeds or spores under specific dynamic conditions and not all the parameter combinations allowed necessarily have realistic counterparts in the plant or microbial worlds.
References
[1] X. Yin, J. Goudriaan, E. A. Lantinga, J. Vos, and H. J. Spiertz, "A Flexible Sigmoid Function of Determinate Growth," Annals of Botany, 91(3), 2003 pp. 361–371.
[2] P. Dantigny, S. P.-M. Nanguy, D. Judet-Correia, and M. Bensoussan, "A New Model for Germination of Fungi," International Journal of Food Microbiology, 146(2), 2011 pp. 176–181.
Permanent Citation